题目内容
经过原点和 (4,0)的两条抛物线
(4,0)的两条抛物线 ,
, ,顶点分别为
,顶点分别为 ,且都在第1象限,连结
,且都在第1象限,连结 交
交 轴于
轴于 ,且
,且 .
.【小题1】分别求出抛物线
 和
和 的解析式;
的解析式;【小题2】点C是抛物线
 的
的 轴上方的一动点,作
轴上方的一动点,作 轴于
轴于 ,交抛物线
,交抛物线 于D,试判断
于D,试判断 和
和 的数量关系,并说明理由;
的数量关系,并说明理由;【小题3】直线
 ,交抛物线
,交抛物线 于M,交抛物线
于M,交抛物线 于N,是否存在以点
于N,是否存在以点 为顶点的四边形是平行四边形,若存在,求出
为顶点的四边形是平行四边形,若存在,求出 的值;若不存在,说明理由..
的值;若不存在,说明理由..
【小题1】∵
 ∴
∴ (2,3),
(2,3), (2,6). ∵
(2,6). ∵ 过
过 (2,3)和
(2,3)和 依题意得:
依题意得: 解得
解得 ∴
∴
同理

【小题2】
 证明;设
证明;设 .∵
.∵ 在
在 上,∴
上,∴
 ∵
∵ 在
在 上,∴
上,∴
 .
.∴
 (
( )—(
)—( )=
)= .
.∴

【小题3】由于MN∥BT,当假设存在四边形
 为平行四边形时,则
为平行四边形时,则 =6.
=6.∵

∴


依题意,得:
 .
.  ="-6, " 此方程无解,
="-6, " 此方程无解, ="6, " 解之得:∴
="6, " 解之得:∴
∴存在
 使得以点
使得以点 为顶点的四边形是平行四边形.解析:
为顶点的四边形是平行四边形.解析:略

练习册系列答案
相关题目
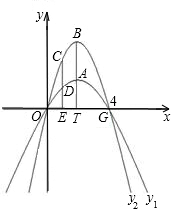 经过原点和G(4,0)的两条抛物线y1=a1x2+b1x,y2=a2x2+b2x,顶点分别为A,B,且都在第1象限,连接BA交x轴于T,且BA=AT=3.
经过原点和G(4,0)的两条抛物线y1=a1x2+b1x,y2=a2x2+b2x,顶点分别为A,B,且都在第1象限,连接BA交x轴于T,且BA=AT=3. 已知:如图,抛物线y=x2+bx+c(b、c为常数)经过原点和E(3,0).
已知:如图,抛物线y=x2+bx+c(b、c为常数)经过原点和E(3,0).