Question

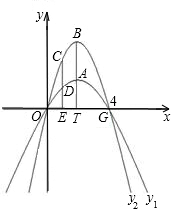经过原点和G（4，0）的两条抛物线y₁=a₁x²+b₁x，y₂=a₂x²+b₂x，顶点分别为A，B，且都在第1象限，连接BA交x轴于T，且BA=AT=3．
（1）分别求出抛物线y₁和y₂的解析式；
（2）点C是抛物线y₂的x轴上方的一动点，作CE⊥x轴于E，交抛物线y₁于D，试判断CD和DE的数量关系，并说明理由；
（3）直线x=m，交抛物线y₁于M，交抛物线y₂于N，是否存在以点M，N，B，T为顶点的四边形是平行四边形，若存在，求出m的值；若不存在，说明理由．

Answer 1

分析：（1）结合图形和已知，可得出A和B点的坐标，又已知G点的坐标，分别代入解析式中，即可得出两函数式的解析式；
（2）根据题意，可分别用含t的表达式将CD和CE表示出，即可得出CD和DE之间的关系．
（3）假设存在四边形BTNM为平行四边形时，分别表示出M和N的坐标，并写出MN的长度，解方程即可得出m的值．

解答：解：（1）∵BA=AT=3，
∴A（2，3），B（2，6）．
∵y₁=a₁x²+b₁x过A（2，3）和G（4，0）．
依题意得：

4a1+2b1=3 16a1+4b1=0

解得

a1=- 3 4 b1=3

∴y1=-

3

4

x2+3x．
同理y2=-

3

2

x2+6x．

（2）CD=ED．
证明；设OE=t，0＜t＜4．
∵D在y1=-

3

4

x2+3x．上，
∴DE=-

3

4

t2+3t．
∵C在y2=-

3

2

x2+6x上，
∴CE=-

3

2

t2+6t．
∴CD=CE-DE=（-

3

2

t2+6t）-（-

3

4

t2+3t）=-

3

4

t2+3t．
∴CD=DE．

（3）由于MN∥BT，当假设存在四边形BTNM为平行四边形时，则BT=MN=6．
∵M(m，-

3

4

m2+3m)，N(m，-

3

2

m2+6m)
∴MN=(-

3

4

m2+3m)-(-

3

2

m2+6m)=

3

4

m2-3m．
依题意，得：6=|

3

4

m2-3m|.

3

4

m2-3m=-6，此方程无解，

3

4

m2-3m=6，
解之得：∴m=2±2

3

．
∴存在m=2±2

3

使得以点M，N，B，T为顶点的四边形是平行四边形．

点评：本题主要考查了二次函数解析式的确定、函数图象交点的求法等知识点．主要考查学生数形结合的数学思想方法．