题目内容
 如图,菱形ABCD的周长为8,两邻角的比为2:1,则对角线的长分别为
如图,菱形ABCD的周长为8,两邻角的比为2:1,则对角线的长分别为考点:菱形的性质
专题:计算题
分析:依题意,根据菱形的性质首先求出边长,然后推出对角线与菱形的两边构成的三角形为等边三角形,最后可解答.
解答:解:∵菱形的周长为8,
∴菱形的边长是:8×
=2,
∵两个邻角的比是1:2,
∴较大的角是120°,较小的角是60°,
∴这个菱形的对角线AC所对的角是60°,
由菱形的性质得到,AC与菱形的两边构成的三角形是等边三角形,
∴AC=2,
BD=2×
×tan60°=2
.
故答案为:2和2
.
∴菱形的边长是:8×
| 1 |
| 4 |
∵两个邻角的比是1:2,
∴较大的角是120°,较小的角是60°,
∴这个菱形的对角线AC所对的角是60°,
由菱形的性质得到,AC与菱形的两边构成的三角形是等边三角形,
∴AC=2,
BD=2×
| AC |
| 2 |
| 3 |
故答案为:2和2
| 3 |
点评:本题考查菱形性质的运用,属于基础题目,根据菱形的性质求出菱形的边长,然后根据等边三角形的性质求解.

练习册系列答案
相关题目
 星期天,小明从家里出发到图书馆去看书,再回到家.他离家的距离y(千米)与时间M分钟)的关系如图所示.小明去图书馆时的速度是
星期天,小明从家里出发到图书馆去看书,再回到家.他离家的距离y(千米)与时间M分钟)的关系如图所示.小明去图书馆时的速度是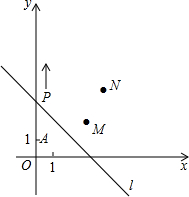 如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒.若点M,N位于直线l的异侧,则t的取值范围是
如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒.若点M,N位于直线l的异侧,则t的取值范围是