题目内容
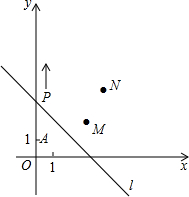如图，A（0，1），M（3，2），N（4，4）．动点P从点A出发，沿y轴以每秒1个单位长的速度向上移动，且过点P的直线l：y=-x+b也随之移动，设移动时间为t秒．若点M，N位于直线l的异侧，则t的取值范围是考点：一次函数图象与几何变换
专题：计算题
分析：分别求出直线l经过点M、点N时的t值，即可得到t的取值范围．
解答：解：当直线y=-x+b过点M（3，2）时，
2=-3+b，
解得：b=5，
5=1+t，
解得t=4．
当直线y=-x+b过点N（4，4）时，
4=-4+b，
解得：b=8，
8=1+t，
解得t=7．
故若点M，N位于l的异侧，t的取值范围是：4＜t＜7．
故答案为：4＜t＜7．
2=-3+b，
解得：b=5，
5=1+t，
解得t=4．
当直线y=-x+b过点N（4，4）时，
4=-4+b，
解得：b=8，
8=1+t，
解得t=7．
故若点M，N位于l的异侧，t的取值范围是：4＜t＜7．
故答案为：4＜t＜7．
点评：本题考查了坐标平面内一次函数的图象与性质，得出直线l经过点M、点N时的t值是解题关键．
练习册系列答案
相关题目
如图，菱形ABCD的周长为8，两邻角的比为2：1，则对角线的长分别为