题目内容
在△ABC中，∠C=90°，BD平分∠ABC，交AC于点D，过点D作DE⊥AB于E，E点恰为AB的中点．若DE=1cm，DB=2cm，求AC的长．考点：角平分线的性质,线段垂直平分线的性质
专题：
分析：先根据角平分线的性质得出CD的长，再根据线段垂直平分线的性质求出AD的长，进而可得出结论．
解答：解：∵在△ABC中，∠C=90°，BD平分∠ABC，交AC于点D，过点D作DE⊥AB，DE=1cm，
∴CD=DE=1cm，
∵E点恰为AB的中点，DB=2cm，
∴ADF=BD=2cm，
∴AC=AD+CD=2+1=3cm．
∴CD=DE=1cm，
∵E点恰为AB的中点，DB=2cm，
∴ADF=BD=2cm，
∴AC=AD+CD=2+1=3cm．
点评：本题考查的是角平分线的性质，熟知角的平分线上的点到角的两边的距离相等是解答此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
已知：点D在AB上，点E在AC上，AB=AC，BE⊥AC，CD⊥AB，求证：BD=CE．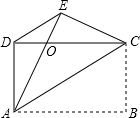
如图，四边形ABCD中，AD=BC，AB=DC，把四边形沿AC折叠，点B落在点E处，AE与DC的交点为O，连接DE．
如图A、B、C是数轴上顺次三点，A，C点对应的数为-1，5．设点B对应的数为b，B，C之间的距离记为BC，A，B之间的距离记为AB．