题目内容
 如图A、B、C是数轴上顺次三点,A,C点对应的数为-1,5.设点B对应的数为b,B,C之间的距离记为BC,A,B之间的距离记为AB.
如图A、B、C是数轴上顺次三点,A,C点对应的数为-1,5.设点B对应的数为b,B,C之间的距离记为BC,A,B之间的距离记为AB.(1)若BC=2AB,求b的值;
(2)在(1)的条件下,点A、B、C开始在数轴上运动,点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度,5个单位长度的速度向右运动,若运动时间为t(秒),请判断:BC-AB的值是否随时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
考点:一元一次方程的应用,数轴,两点间的距离
专题:
分析:(1)根据数轴上的点表示出AB、BC,然后列出方程求解即可;
(2)根据向右平移加,向左平移减表示出AB、BC,然后代入BC-AB整理即可得解.
(2)根据向右平移加,向左平移减表示出AB、BC,然后代入BC-AB整理即可得解.
解答:解:(1)∵A,C点对应的数为-1,5,点B对应的数为b,
∴AB=b-(-1)=b+1,BC=5-b,
∵BC=2AB,
∴5-b=2(b+1),
解得b=1;
(2)由(1)知AB=2,BC=4,
∵点A以每秒1个单位长度的速度向左运动,点B和点C分别以每秒2个单位长度,5个单位长度的速度向右运动,
∴AB=2+3t,BC=4+(5-2)t=4+3t,
∴BC-AB=(4+3t)-(2+3t)=2,为定值,
∴BC-AB=2,不随时间t的变化而改变.
∴AB=b-(-1)=b+1,BC=5-b,
∵BC=2AB,
∴5-b=2(b+1),
解得b=1;
(2)由(1)知AB=2,BC=4,
∵点A以每秒1个单位长度的速度向左运动,点B和点C分别以每秒2个单位长度,5个单位长度的速度向右运动,
∴AB=2+3t,BC=4+(5-2)t=4+3t,
∴BC-AB=(4+3t)-(2+3t)=2,为定值,
∴BC-AB=2,不随时间t的变化而改变.
点评:本题考查了一次方程的应用,熟练掌握数轴上两点间的距离的表示方法,分别表示出AB、BC是解题的关键,也是本题的难点.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 如图所示,已知点E、F、D在同一条直线上,AF=DE,AB⊥DC,CE⊥AD,垂足分别为F、E,AB=DC,求证:AB∥CD.
如图所示,已知点E、F、D在同一条直线上,AF=DE,AB⊥DC,CE⊥AD,垂足分别为F、E,AB=DC,求证:AB∥CD. 在△ABC中,∠C=90°,BD平分∠ABC,交AC于点D,过点D作DE⊥AB于E,E点恰为AB的中点.若DE=1cm,DB=2cm,求AC的长.
在△ABC中,∠C=90°,BD平分∠ABC,交AC于点D,过点D作DE⊥AB于E,E点恰为AB的中点.若DE=1cm,DB=2cm,求AC的长.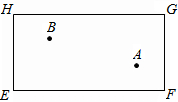 如图,四边形EFGH为长方形的台球桌面,现有一白球A和一彩球B,在图中的GH边上找一点O,当击打白球A时,使白球A碰撞台边GH上的O点,反弹后能击中彩球B.
如图,四边形EFGH为长方形的台球桌面,现有一白球A和一彩球B,在图中的GH边上找一点O,当击打白球A时,使白球A碰撞台边GH上的O点,反弹后能击中彩球B. 在正方形ABCD各边上一次截取AE=BF=CG=DH,连接EF,FG,GH,HE.试问四边形EFGH是否是正方形?
在正方形ABCD各边上一次截取AE=BF=CG=DH,连接EF,FG,GH,HE.试问四边形EFGH是否是正方形?