题目内容
12．设梯形ABCD中，AB∥CD，E，F分别在腰AD和BC上，若A，B，F，E四点共圆，证明C，D，E，F也必四点共圆．分析 连接EF，根据圆内接四边形的性质得到∠A=∠EFC，根据平行线的性质得到∠A+∠D=180°，得到∠EFC+∠D=180°，证明C，D，E，F四点共圆．
解答 证明：
连接EF，
∵A，B，F，E四点共圆，
∴∠A=∠EFC，
∵AB∥CD，
∴∠A+∠D=180°，
∴∠EFC+∠D=180°，
∴C，D，E，F四点共圆．
点评 本题考查的是四点共圆问题，掌握一个四边形，若对角互补，那么这四点共圆是解题的关键．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
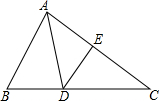如图，在△ABC中，已知边AC的垂直平分线DE交BC于点D，连接AD，若BC=5，AB=3，则△ABD的周长为8．
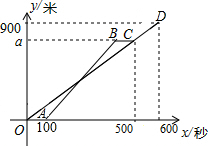小明、小亮从宝安中心图书馆出发，沿相同的线路跑向宝安体育场，小明先跑一点路程后，小亮开始出发，当小亮超过小明150米时，小亮停在此地等候小明，两人相遇后，一起以小明原来的速度跑向宝安体育场，如图，反映了两人所跑路程y（米）与所用时间x（秒）之间的关系，请根据题意解答下列问题：
2．与$\sqrt{2}$-$\sqrt{3}$互为倒数的是（ ）
| A． | $\sqrt{2}$+$\sqrt{3}$ | B． | $\sqrt{2}$-$\sqrt{3}$ | C． | $\sqrt{3}$-$\sqrt{2}$ | D． | -$\sqrt{2}$-$\sqrt{3}$ |