题目内容
 已知△ABC,△ADE均为等腰直角三角形,且∠BAC=∠DAE=90°,BD的延长线交AC于点F,交CE于G.
已知△ABC,△ADE均为等腰直角三角形,且∠BAC=∠DAE=90°,BD的延长线交AC于点F,交CE于G.(1)求证:BD⊥CE;
(2)连接AG,求证:EG+DG=
| 2 |
考点:全等三角形的判定与性质,等腰直角三角形
专题:证明题
分析:(1)证明△ABD≌△ACE,得到∠ABD=∠ACE,借助等腰直角三角形的性质,即可解决问题.
(2)如图,作辅助线;证明A、D、G、E四点共圆,得到∠AGD=∠AED=45°,证明△ADM≌△AEN,得到DM=EN;同理可证GM=GN,得到GN=
;证明AN=GN,借助勾股定理即可解决问题.
(2)如图,作辅助线;证明A、D、G、E四点共圆,得到∠AGD=∠AED=45°,证明△ADM≌△AEN,得到DM=EN;同理可证GM=GN,得到GN=
| GD+GE |
| 2 |
解答: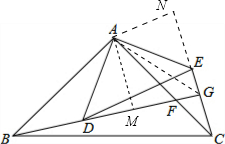 证明:(1)∵△ABC,△ADE均为等腰直角三角形,
证明:(1)∵△ABC,△ADE均为等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE,
∴∠BAD=∠CAE;在△ABD与△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
∴∠GBC+∠GCB=∠ABC+∠ACB=90°,
∴BD⊥CE.
(2)如图,连接AG;过点A作AM⊥DG,
AN⊥GE,交GE的延长线于点N;
设AG=λ,GD=μ,GE=γ;
∵∠DAE+∠DGE=180°,
∴A、D、G、E四点共圆,
∴∠AGD=∠AED=45°,
∠AGE=∠ADE=45°,
∠AEN=∠ADM;
∴AG平分∠DGN,
∴AM=AN;在△ADM与△AEN中,
,
∴△ADM≌△AEN(HL),
∴DM=EN(设为λ);同理可证:GM=GN(设为μ),
即GD=λ+μ,GE=μ-λ,
∴λ=
,GN=GE+λ=
;
∵∠AGN=45°,∠N=90°,
∴∠NAG=∠AGN=45°,
∴AN=GN;由勾股定理得:AG2=2GN2,
∴EG+DG=
AG.
 证明:(1)∵△ABC,△ADE均为等腰直角三角形,
证明:(1)∵△ABC,△ADE均为等腰直角三角形,∴AB=AC,AD=AE,∠BAC=∠DAE,
∴∠BAD=∠CAE;在△ABD与△ACE中,
|
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
∴∠GBC+∠GCB=∠ABC+∠ACB=90°,
∴BD⊥CE.
(2)如图,连接AG;过点A作AM⊥DG,
AN⊥GE,交GE的延长线于点N;
设AG=λ,GD=μ,GE=γ;
∵∠DAE+∠DGE=180°,
∴A、D、G、E四点共圆,
∴∠AGD=∠AED=45°,
∠AGE=∠ADE=45°,
∠AEN=∠ADM;
∴AG平分∠DGN,
∴AM=AN;在△ADM与△AEN中,
|
∴△ADM≌△AEN(HL),
∴DM=EN(设为λ);同理可证:GM=GN(设为μ),
即GD=λ+μ,GE=μ-λ,
∴λ=
| GD-GE |
| 2 |
| GD+GE |
| 2 |
∵∠AGN=45°,∠N=90°,
∴∠NAG=∠AGN=45°,
∴AN=GN;由勾股定理得:AG2=2GN2,
∴EG+DG=
| 2 |
点评:该题主要考查了全等三角形的判定及其性质、等腰直角三角形的性质、勾股定理等几何知识点的应用问题;解题的关键是作辅助线;牢固掌握定理内容,灵活运用有关定理来分析、判断.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
英国曼彻斯热大学的两位科学家因为成功地从石墨中分离出石墨烯,荣获 诺贝尔物理学奖.石墨烯目前是世界上最薄却也是最坚硬的纳米材料,同时还是导电性最好的材料,其理论厚度仅0.000000000034米,将这个数用科学记数法表示为( )
| A、0.34×10-5 |
| B、3.4×10-4 |
| C、3.4×10-14 |
| D、3.4×10-11 |
 如图,从棱长为2的正方体毛柸的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件,分别画出从正面、从左面和从上面看到的平面图.
如图,从棱长为2的正方体毛柸的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件,分别画出从正面、从左面和从上面看到的平面图.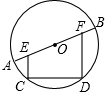 如图,AB是直径,CD是弦,过点C和D作EC⊥CD、FD⊥CD,分别交AB于点E、F.试猜想:AE与BF是何关系.说明理由.
如图,AB是直径,CD是弦,过点C和D作EC⊥CD、FD⊥CD,分别交AB于点E、F.试猜想:AE与BF是何关系.说明理由.