题目内容
 如图,在△ABC中,AB=13,BC=10,BC边上的中线AD=12,试判定△ABC的形状( )
如图,在△ABC中,AB=13,BC=10,BC边上的中线AD=12,试判定△ABC的形状( )| A、直角三角形 |
| B、等边三角形 |
| C、等腰三角形 |
| D、以上都不对 |
考点:勾股定理的逆定理,等腰三角形的判定
专题:
分析:在△ABD中,根据勾股定理的逆定理即可判断AD⊥BC,然后根据线段的垂直平分线的性质,即可得到AC=AB,从而求解.
解答:解:∵AD是中线,AB=13,BC=10,
∴BD=
BC=5.
∵52+122=132,即BD2+AD2=AB2,
∴△ABD是直角三角形,则AD⊥BC,
又∵BD=CD,
∴AC=AB=13,
∴△ABC的形状是等腰三角形,
故选:C.
∴BD=
| 1 |
| 2 |
∵52+122=132,即BD2+AD2=AB2,
∴△ABD是直角三角形,则AD⊥BC,
又∵BD=CD,
∴AC=AB=13,
∴△ABC的形状是等腰三角形,
故选:C.
点评:本题主要考查了勾股定理的逆定理与线段的垂直平分线的性质,关键是利用勾股定理的逆定理证得AD⊥BC.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列数轴的画法中正确的是( )
A、 |
B、 |
C、 |
D、 |
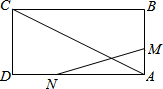 如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以每秒1cm的速度向B点匀速运动;同时,动点N从D点出发沿DA方向以每秒2cm的速度向A点匀速运动.设出发时间为t秒,△AMN的面积为S(cm2).
如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以每秒1cm的速度向B点匀速运动;同时,动点N从D点出发沿DA方向以每秒2cm的速度向A点匀速运动.设出发时间为t秒,△AMN的面积为S(cm2).