题目内容
6.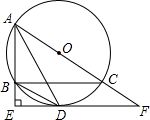 在△AEF中,∠E=90°,AD为∠EAF的平分线,过A、D的⊙O与AE、AF分别交于B、C,且BC∥EF
在△AEF中,∠E=90°,AD为∠EAF的平分线,过A、D的⊙O与AE、AF分别交于B、C,且BC∥EF(1)求证:AC为⊙O的直径;
(2)求证:EF与⊙O的相切;
(3)若sin∠ADB=$\frac{3}{5}$,BE=1,求⊙O的半径.
分析 (1)根据平行线的性质,由BC∥EF得到∠ABC=∠E=90°,然后根据圆周角定理的推论即可得到AC为⊙O的直径;
(2)连结OD,如图,根据平行线的判定方法证明OD∥AE,从而得到∠ODF=∠E=90°,然后根据切线的判定定理可得EF与⊙O的相切;
(3)OD与BC交于H,易得四边形BEDH为矩形,则DH=BE=1,设⊙O的半径为r,则OC=r,OH=r-1,根据圆周角定理得到∠ACB=∠ADB,则sin∠ACB=sin∠ADB=$\frac{3}{5}$,然后在Rt△OHC中利用正弦的定义得到sin∠OCH=$\frac{OH}{OC}$=$\frac{3}{5}$,即$\frac{r-1}{r}$=$\frac{3}{5}$,再利用比例性质求r即可.
解答  (1)证明:∵BC∥EF,
(1)证明:∵BC∥EF,
∴∠ABC=∠E=90°,
∴AC为⊙O的直径;
(2)证明:连结OD,如图,
∵AD为∠EAF的平分线,
∴∠1=∠2,
∵OA=OD,
∴∠2=∠ODA,
∴∠1=∠ODA,
∴OD∥AE,
∴∠ODF=∠E=90°,
∴OD⊥EF,
∴EF与⊙O的相切;
(3)解:OD与BC交于H,易得四边形BEDH为矩形,则DH=BE=1,
设⊙O的半径为r,则OC=r,OH=OD-DH=r-1,
∵∠ACB=∠ADB,
∴sin∠ACB=sin∠ADB=$\frac{3}{5}$,
在Rt△OHC中,∵sin∠OCH=$\frac{OH}{OC}$=$\frac{3}{5}$,
∴$\frac{r-1}{r}$=$\frac{3}{5}$,解得r=$\frac{5}{2}$,
即⊙O的半径为$\frac{5}{2}$.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了圆周角定理.


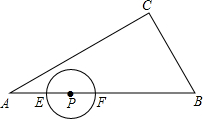 如图,在Rt△ABC中,∠C=90°,BC=3,∠A=30°,点P在AB上,AP=2.点E、F同时从点P出发,分别沿PA、PB以每秒1个单位长度的速度向点A、B匀速运动,点E到达点A后立刻以原速度沿AB向点B运动,点F运动到点B时停止,点E也运动到点B时停止.在点E、F运动过程中,以EF为直径作圆.设点E运动的时间为t秒.
如图,在Rt△ABC中,∠C=90°,BC=3,∠A=30°,点P在AB上,AP=2.点E、F同时从点P出发,分别沿PA、PB以每秒1个单位长度的速度向点A、B匀速运动,点E到达点A后立刻以原速度沿AB向点B运动,点F运动到点B时停止,点E也运动到点B时停止.在点E、F运动过程中,以EF为直径作圆.设点E运动的时间为t秒.