题目内容
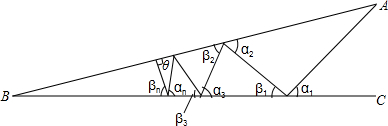
如图所示,已知∠ABC=8°,∠θ=90°.若∠α1=∠β1,∠α2=∠β2,∠α3=∠β3,…,∠αn=∠βn(n是大于等于1的自然数),试探究∠A的度数x与n的关系式.

考点:三角形内角和定理
专题:规律型
分析:求得n=1、2、3、…时的∠A的值,发现规律,即可求得∠A的度数x与n的关系式.
解答:解:∵∠ABC=8°,∠θ=90°.若∠α1=∠β1,∠α2=∠β2,∠α3=∠β3,…,∠αn=∠βn,
∴当n=1时,∠A=90°-8°-8°=90°-2×8°,
当n=2时,∠A=90°-3×8°,
当n=3时,∠A=90°-4×8°,
…
所以,x=90°-(n+1)•8°.
∴当n=1时,∠A=90°-8°-8°=90°-2×8°,
当n=2时,∠A=90°-3×8°,
当n=3时,∠A=90°-4×8°,
…
所以,x=90°-(n+1)•8°.
点评:本题考查了三角形的内角和定理和三角形外角的性质,找出规律是本题的关键.

练习册系列答案
相关题目
某班男生比女生多
,男生相当于全班人数的( )
| 3 |
| 8 |
A、
| ||
B、
| ||
C、
| ||
D、
|

 一把纸折扇完全打开后,外侧两竹条AB和AC的夹角为120°,AD长为5cm,AB为15cm,求两面贴纸部分的面积的面积.
一把纸折扇完全打开后,外侧两竹条AB和AC的夹角为120°,AD长为5cm,AB为15cm,求两面贴纸部分的面积的面积.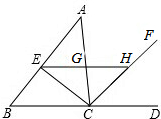 已知:如图,∠ACD是△ABC的一个外角,CE、CF分别平分∠ACB、∠ACD,EH∥BC,分别交AC、CF于点G、H.求证:GE=GH.
已知:如图,∠ACD是△ABC的一个外角,CE、CF分别平分∠ACB、∠ACD,EH∥BC,分别交AC、CF于点G、H.求证:GE=GH. 小华用透明的纸糊的四边形风筝.糊好后用手边的量角器测量发现,无论支架AB与CD有多长,只要满足DA=DB,CA=CB,∠CAD与∠CBD总是相等的,为什么?
小华用透明的纸糊的四边形风筝.糊好后用手边的量角器测量发现,无论支架AB与CD有多长,只要满足DA=DB,CA=CB,∠CAD与∠CBD总是相等的,为什么?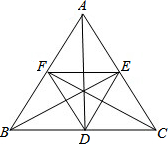 已知:如图,AB、BE、CF是等边△ABC的角平分线.求证:△DEF是等边三角形.
已知:如图,AB、BE、CF是等边△ABC的角平分线.求证:△DEF是等边三角形.