题目内容
9.计算$\sqrt{\frac{1}{2}}$-$\sqrt{8}$的结果是( )| A. | $-\frac{3}{2}$$\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | $-\sqrt{2}$ | D. | $-\frac{7}{2}$$\sqrt{2}$ |
分析 首先化二次根式,进而合并得出答案.
解答 解:$\sqrt{\frac{1}{2}}$-$\sqrt{8}$
=$\frac{\sqrt{2}}{2}$-2$\sqrt{2}$
=-$\frac{3}{2}$$\sqrt{2}$.
故选:A.
点评 此题主要考查了二次根式的加减运算,正确化简二次根式是解题关键.

练习册系列答案
相关题目
19.下列各式运算正确的是( )
| A. | 2a+3b=5ab | B. | -2x2-x2=-3x4 | C. | -1.5-2$\frac{1}{2}$=-4 | D. | -32=(-3)2 |
20.下列计算中正确的是( )
| A. | $\sqrt{(-2)^{2}}$=-2 | B. | $\sqrt{2}×\sqrt{8}$=4 | C. | ($\sqrt{-2}$)2=-2 | D. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ |
17. 如图所示,矩形ABCD中,AB=4,BC=$4\sqrt{3}$,点E是折线ADC上的一个动点(点E与点A不重合),点P是点A关于BE的对称点.在点E运动的过程中,使△PCB为等腰三角形的点E的位置共有( )
如图所示,矩形ABCD中,AB=4,BC=$4\sqrt{3}$,点E是折线ADC上的一个动点(点E与点A不重合),点P是点A关于BE的对称点.在点E运动的过程中,使△PCB为等腰三角形的点E的位置共有( )
 如图所示,矩形ABCD中,AB=4,BC=$4\sqrt{3}$,点E是折线ADC上的一个动点(点E与点A不重合),点P是点A关于BE的对称点.在点E运动的过程中,使△PCB为等腰三角形的点E的位置共有( )
如图所示,矩形ABCD中,AB=4,BC=$4\sqrt{3}$,点E是折线ADC上的一个动点(点E与点A不重合),点P是点A关于BE的对称点.在点E运动的过程中,使△PCB为等腰三角形的点E的位置共有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
4.已知正方形ABCD的边长为1,以AC为边作等边三角形ACE,过点E作AD边的垂线交AD的延长线于点F,则EF的长为( )
| A. | $\frac{2-\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}-1}{2}$ | C. | $\sqrt{2}$-1 | D. | 2-$\sqrt{2}$ |
1.在平面直角坐标系xOy中,如果⊙O是以原点O(0,0)为圆心,以5为半径的圆,那么点A(-3,-4)与⊙O的位置关系是( )
| A. | 在⊙O内 | B. | 在⊙O上 | C. | 在⊙O外 | D. | 不能确定 |
19.某居民小区开展节约用电活动,对该小区30户家庭的节电量情况进行了统计,五月份与四月份相比,节电情况如下表:
则五月份这30户家庭节电量的众数与中位数分别为( )
| 节电量(度) | 10 | 20 | 30 | 40 |
| 户数 | 2 | 15 | 10 | 3 |
| A. | 20,20 | B. | 20,25 | C. | 30,25 | D. | 40,20 |
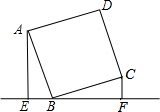 如图,直线L过正方形ABCD的顶点B,点A、点C到直线L的距离分别是2和1,求正方形ABCD的边长?
如图,直线L过正方形ABCD的顶点B,点A、点C到直线L的距离分别是2和1,求正方形ABCD的边长?


