题目内容
 如图,△ABC是直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,能与△ACP′重合,求证:PP′=
如图,△ABC是直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,能与△ACP′重合,求证:PP′=| 2 |
考点:旋转的性质,等腰直角三角形
专题:证明题
分析:根据旋转的性质得AP=AP′,∠PAP′=∠BAC=90°,则可判断△APP′为等腰直角三角形,于是有PP′=
AP.
| 2 |
解答:证明:∵△ABC是直角三角形,BC是斜边,
∴∠BAC=90°,
∵△ABP绕点A逆时针旋转后,能与△ACP′重合,
∴AP=AP′,∠PAP′=∠BAC=90°,
∴△APP′为等腰直角三角形,
∴PP′=
AP.
∴∠BAC=90°,
∵△ABP绕点A逆时针旋转后,能与△ACP′重合,
∴AP=AP′,∠PAP′=∠BAC=90°,
∴△APP′为等腰直角三角形,
∴PP′=
| 2 |
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰直角三角形的判定与性质.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目

 如图,⊙O的半径为
如图,⊙O的半径为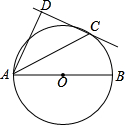 如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB.
如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB.