题目内容
【题目】如图,在扇形AOB中,∠AOB=120°,连接AB,以OA为直径作半圆C交AB于点D,若OA=6,则图中阴影部分的面积为_____.

【答案】![]()
【解析】
连接OD、CD,根据圆周角定理得到OD⊥AB,根据等腰三角形的性质得到AD=DB,∠OAD=30°,根据扇形面积公式、三角形的面积公式计算即可.
连接OD、CD,
∵OA为圆C的直径,
∴OD⊥AB,
∵OA=OB,∠AOB=120°,
∴AD=DB,∠OAD=30°,
∴OD=![]() OA=3,
OA=3,
由勾股定理得,AD=![]() =3
=3![]() ,
,
∴S△AOB=![]() ×AB×OD=9
×AB×OD=9![]() ,
,
∵OC=CA,BD=DA,
∴CD∥OB,CD=![]() OB,
OB,
∴∠ACD=∠AOB=120°,
∴△ACD∽△AOB,且相似比为1:2,
∴S△ACD=![]() S△AOB=
S△AOB=![]() ,
,
∴S阴影=S扇形AOB-S△AOB-(S扇形ACD-S△ACD)
=
=12π﹣9![]() ﹣3π+
﹣3π+![]()
=9π﹣![]() ,
,
故答案为:9π﹣![]() .
.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
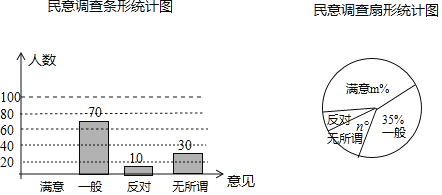
【题目】学习一定要讲究方法,比如有效的预习可大幅提高听课效率.九年级(1)班学习兴趣小组为了了解全校九年级学生的预习情况,对该校九年级学生每天的课前预习时间(单位:![]() )进行了抽样调查.并将抽查得到的数据分成5组,下面是未完成的频数、顿率分布表和频数分布扇形图.
)进行了抽样调查.并将抽查得到的数据分成5组,下面是未完成的频数、顿率分布表和频数分布扇形图.
组别 | 课前预习时间 | 频数(人数) | 频率 |
1 |
| 2 | |
2 |
|
| 0.10 |
3 |
| 16 | 0.32 |
4 |
|
|
|
5 |
| 3 |
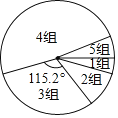
请根据图表中的信息,回答下列问题:
(1)本次调查的样本容量为 ,表中的![]() ,
,![]() ,
,![]() ;
;
(2)试计算第4组人数所对应的扇形圆心角的度数;
(3)该校九年级其有1000名学生,请估计这些学生中每天课前预习时间不少于![]() 的学生人数.
的学生人数.