题目内容
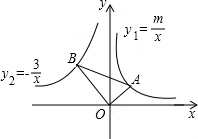 如图,在平面直角坐标系中,∠OAB=60°,∠AOB=90°,反比例函数y1=
如图,在平面直角坐标系中,∠OAB=60°,∠AOB=90°,反比例函数y1=| m |
| x |
| 3 |
| x |
考点:相似三角形的判定与性质,反比例函数图象上点的坐标特征
专题:
分析:根据题意,作BH⊥x轴,AM⊥y轴,∠OAB=60°,∠AOB=90°,∴△BHO∽△AMO,有
=
=
=
,令OM=a,则BH=
a,代入反比例函数y2=-
得:x=-
,所以OH=
,得:AM=
,所以AM•OM=
•a=1,可求得m的值.
| BH |
| OM |
| OH |
| AM |
| BO |
| AO |
| ||
| 1 |
| 3 |
| 3 |
| x |
| ||
| a |
| ||
| a |
| 1 |
| a |
| 1 |
| a |
解答: 解:作BH⊥x轴,垂足为H,AM⊥y轴,垂足为M,
解:作BH⊥x轴,垂足为H,AM⊥y轴,垂足为M,
∵∠OAB=60°,∠AOB=90°,
∴△BHO∽△AMO,
∴
=
=
=
,
令OM=a,则BH=
a,
代入反比例函数y2=-
得:x=-
,
∴OH=
,得:AM=
,
∴AM•OM=
•a=1,
又∵AM•OM=m,
∴m=1.
故答案为1.
 解:作BH⊥x轴,垂足为H,AM⊥y轴,垂足为M,
解:作BH⊥x轴,垂足为H,AM⊥y轴,垂足为M,∵∠OAB=60°,∠AOB=90°,
∴△BHO∽△AMO,
∴
| BH |
| OM |
| OH |
| AM |
| BO |
| AO |
| ||
| 1 |
令OM=a,则BH=
| 3 |
代入反比例函数y2=-
| 3 |
| x |
| ||
| a |
∴OH=
| ||
| a |
| 1 |
| a |
∴AM•OM=
| 1 |
| a |
又∵AM•OM=m,
∴m=1.
故答案为1.
点评:本题考查了反比例函数的解析式的求法,解答本题的关键是用三角形相似的判定,确定边的对应比值,采用设参数的方法进行讲解,学会整体思想求解方程是解题的关键.

练习册系列答案
相关题目
已知圆锥的底面半径为2cm,母线长为5cm,则此圆锥的侧面积为( )
| A、5πcm2 |
| B、10πcm2 |
| C、14πcm2 |
| D、20πcm2 |
 小明家今年种植樱桃喜获丰收,采摘上市20天全部销售完,小明对销售情况进行了跟踪记录,并将记录情况绘成图表.日销售量y(单位:kg)与上市时间x(单位:天)的函数关系如图所示,樱桃单价w(单位:元/kg)与上市时间x(单位:天)的函数关系列表所示,第1天到第a天的单价相同,第a天之后,单价下降,w与x之间是一次函数关系.
小明家今年种植樱桃喜获丰收,采摘上市20天全部销售完,小明对销售情况进行了跟踪记录,并将记录情况绘成图表.日销售量y(单位:kg)与上市时间x(单位:天)的函数关系如图所示,樱桃单价w(单位:元/kg)与上市时间x(单位:天)的函数关系列表所示,第1天到第a天的单价相同,第a天之后,单价下降,w与x之间是一次函数关系. 如图,矩形ABCD中,AD=2AB,E、F分别是AD、BC上的点,线段EF过矩形对角线AC的中点O,且EF⊥AC,PF∥AC,则EF:PE的值是
如图,矩形ABCD中,AD=2AB,E、F分别是AD、BC上的点,线段EF过矩形对角线AC的中点O,且EF⊥AC,PF∥AC,则EF:PE的值是 如图,以AB为直径的半圆O上有两点D、E,ED与BA的延长线交于点C,且有DC=OE,若∠C=20°,则∠EOB的度数是
如图,以AB为直径的半圆O上有两点D、E,ED与BA的延长线交于点C,且有DC=OE,若∠C=20°,则∠EOB的度数是