题目内容
直角三角形两条直角边的长分别为8，15，则斜边上的高为 ．
考点：勾股定理
专题：
分析：设斜边上的高为h，先根据勾股定理求出斜边的长，再由三角形的面积公式即可得出结论．
解答：解：设斜边上的高为h，
∵直角三角形两条直角边的长分别为8，15，
∴斜边的长=
=17，
∴8×15=17h，
解得h=
．
故答案为：
．
∵直角三角形两条直角边的长分别为8，15，
∴斜边的长=
| 82+152 |
∴8×15=17h，
解得h=
| 120 |
| 17 |
故答案为：
| 120 |
| 17 |
点评：本题考查了利用勾股定理及利用面积法求直角三角形的高，是解此类题目常用的方法．
练习册系列答案
相关题目
有下面四包小包装火腿，按规定超过标准克数（200g）的记作正数，不足标准克数的记作负数．其中，最接近标准的是（ ）
| A、+2 | B、-3 | C、+3 | D、-1 |
下列各式：-
a2b2，
x-1，-25，
，
，π，
，a2-2ab+b2，
中单项式的个数有（ ）
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| x |
| x-y |
| 2 |
| 2a |
| y | ||
|
| A、5个 | B、4个 | C、3个 | D、2个 |
如图，在一个半径为2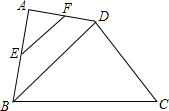
在四边形ABCD中，BD是对角线，E，F分别是AB，AD的中点，若EF=2，tan∠DBC=