Question

11．如图1，AB为⊙O的直径，C为⊙O上一点，作AD⊥CD，垂足为D．
（1）若直线CD与⊙O相切于点C，求证：△ADC∽△ACB；
（2）如果把直线CD向下平行移动，如图2，直线CD交⊙O于C、G两点，若题目中的其他条件不变，tan∠DAC=$\frac{3}{4}$，AB=10，求圆心O到GB的距离OH的长．

Answer 1

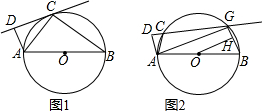
分析 （1）首先连接OC，由CD切⊙O于C，根据切线的性质，可得OC⊥CD，又由AD⊥CD，可得OC∥AD，又由OA=OC，易证得∠DAC=∠CAO，根据圆周角定理求得∠ACB=90°，得出∠ADC=∠ACB，即可证得结论；
（2）由于四边形ABGC为⊙O的内接四边形，根据圆的内接四边形的性质得∠B+∠ACG=180°，易得∠ACD=∠B，又∠ADC=∠AGB=90°，利用等角的余角相等得到∠DAC=∠GAB，根据tan∠DAC=$\frac{3}{4}$=tan∠GAB=$\frac{GB}{AG}$和勾股定理求得AG=8，GB=6，然后求得△ABG∽△OBH，根据相似三角形的性质求得$\frac{OB}{AB}$=$\frac{OH}{AG}$=$\frac{1}{2}$，即可求得OH=4．

解答 （1）证明：连接OC，如图1，
∵直线CD与⊙O相切于点C，
∴OC⊥CD，
∵AD⊥CD，
∴AD∥OC，
∴∠DAC=∠ACO，
∵OA=OC，
∴∠ACO=∠CAO，
∴∠DAC=∠CAO，
∵AB为⊙O的直径，
∴∠ACB=90°，
∴∠ADC=∠ACB，
∴△ADC∽△ACB；
（2）解：如图2，∵AB是⊙O的直径，
∴∠AGB=90°，
∵四边形ABGC是⊙O的内接四边形，
∴∠ACD=∠B，
∵∠ADC=∠AGB=90°，
∴∠DAC=∠GAB，
∵tan∠DAC=$\frac{3}{4}$=tan∠GAB=$\frac{GB}{AG}$，
设GB=3x，AG=4x，
∵AB=10，
∴（3x）²+（4x）²=10²，
解得x=2，
∴AG=8，GB=6，
∵OH⊥GB，AG⊥GB，
∴OH∥AG，
∴△ABG∽△OBH，
∴$\frac{OB}{AB}$=$\frac{OH}{AG}$=$\frac{1}{2}$，
∴OH=4．

点评 此题考查了切线的性质、垂径定理、等腰三角形的性质、平行线的判定与性质以及相似三角形的判定与性质．此题难度适中，注意掌握辅助线的作法，注意数形结合思想的应用．