题目内容
20. 如图,四边形ABCD为正方形,点A、B在y轴上,点C的坐标为(-3,1),反比例函数y=$\frac{k}{x}$的图象经过点D,则k的值为6.
如图,四边形ABCD为正方形,点A、B在y轴上,点C的坐标为(-3,1),反比例函数y=$\frac{k}{x}$的图象经过点D,则k的值为6.
分析 先依据正方形的性质求得点D的坐标,然后再将点D的坐标代入反比例函数的解析式,从而求得k的值.
解答 解:∵C(-3,1),
∴BC=3.
∵ABCD为正方形,
∴DC=3.
∴D(-3,-2).
∴k=-3×(-2)=6.
故答案为:6.
点评 本题主要考查的是正方形的性质,待定系数法求反比例函数的解析式,求得点D的坐标是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
10.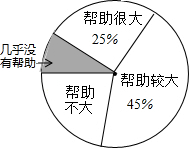 为了解“数学思想作文对学习数学帮助有多大?”研究员随机抽取了一定数量的高校大一学生进行了问卷调查,并将调查得到的数据用下面的扇形图和表1来表示(图、表都没制作完成).
为了解“数学思想作文对学习数学帮助有多大?”研究员随机抽取了一定数量的高校大一学生进行了问卷调查,并将调查得到的数据用下面的扇形图和表1来表示(图、表都没制作完成).
表1
根据上面图、表提供的信息,解决下列问题:
(1)这次共有多少名学生参加了问卷调查?
(2)求a、b的值.
 为了解“数学思想作文对学习数学帮助有多大?”研究员随机抽取了一定数量的高校大一学生进行了问卷调查,并将调查得到的数据用下面的扇形图和表1来表示(图、表都没制作完成).
为了解“数学思想作文对学习数学帮助有多大?”研究员随机抽取了一定数量的高校大一学生进行了问卷调查,并将调查得到的数据用下面的扇形图和表1来表示(图、表都没制作完成).表1
| 选项 | 帮助很大 | 帮助较大 | 帮助不大 | 几乎没有帮助 |
| 人数 | a | 540 | 270 | b |
(1)这次共有多少名学生参加了问卷调查?
(2)求a、b的值.
15. 已知一次函数y=(a+1)x+b的图象如图所示,那么a的取值范围是( )
已知一次函数y=(a+1)x+b的图象如图所示,那么a的取值范围是( )
 已知一次函数y=(a+1)x+b的图象如图所示,那么a的取值范围是( )
已知一次函数y=(a+1)x+b的图象如图所示,那么a的取值范围是( )| A. | a>1 | B. | a<-1 | C. | a>-1 | D. | a<0 |
5.今年,我市全面启动“精准扶贫”工作,某校为了了解九年级贫困生人数,对该校九年级6个班进行摸排,得到各班贫困生人数分别为12,12,14,10,18,16,这组数据的众数和中位数分别是( )
| A. | 12和10 | B. | 12和13 | C. | 12和12 | D. | 12和14 |
12. 如图,AB∥CD,CB∥DE,若∠B=72°,则∠D的度数为( )
如图,AB∥CD,CB∥DE,若∠B=72°,则∠D的度数为( )
 如图,AB∥CD,CB∥DE,若∠B=72°,则∠D的度数为( )
如图,AB∥CD,CB∥DE,若∠B=72°,则∠D的度数为( )| A. | 36° | B. | 72° | C. | 108° | D. | 118° |
9.若正六边形的半径长为4,则它的边长等于( )
| A. | 4 | B. | 2 | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
 如图,线段AB,C是线段AB上一点,M是AB的中点,N是AC的中点.
如图,线段AB,C是线段AB上一点,M是AB的中点,N是AC的中点.
