题目内容
19.如图1,Rt△ACB中,∠ACB=90°,∠A=30°,BC=2,P为AB的中点,以P为直角顶点的等腰Rt△PDE,PE与AC交于M,PD与直线BC交于N.
(1)求证:AM2+BN2=MN2
(2)若AM=x,BN=y,求y与x之间的函数关系式(利用图2作答).
(3)若将等腰Rt△PDE绕点P旋转,当PE恰好经过点C时,延长EP交AN于F,如图3,求PF的长.
分析 (1)如图1,延长MP至E,且使PE=MP,构建全等三角形△MPA≌△EPB(SAS)和△MPN≌△DPN(SAS),由全等三角形的对应边相等得到:MN=EN,所以在Rt△BDN中,利用勾股定理证得结论;
(2)根据含30度角的直角三角形ABC的性质求得AB、AC的长度;然后在Rt△MCN中利用勾股定理列出关于关于x、y的方程,整理后即可得到答案;
(3)根据题意推知△PCB为等边三角形,易得PN=2$\sqrt{3}$,过点A作AG⊥EF于G.利用面积法来求PF的长度:S△FCN=2S△AFC,S△FCN=$\frac{2}{3}$S△ACN=$\frac{2\sqrt{3}}{3}$=$\frac{1}{2}$×CF×2$\sqrt{3}$.
解答  解:(1)延长MP至E,且使PE=MP,
解:(1)延长MP至E,且使PE=MP,
可证:△MPA≌△EPB(SAS),
∴∠MAP=∠DBO,MA=DB.
∵∠MAP+∠ABC=∠DBO+∠ABC=90°,
可证:△MPN≌△DPN(SAS),
∴MN=EN,
在Rt△BDN中,DN2=BN2+BD2,
∴AM2+BN2=MN2;
(2)如图2,∵∠A=30°,BC=2,
∴AB=4,AC=2$\sqrt{3}$,
∴MC=2$\sqrt{3}$-x,NC=2-y,
在Rt△MCN中,MN2=MC2+NC2,
∴x2+y2=(2$\sqrt{3}$-x)2+(2-y)2,化简得:y=-$\sqrt{3}$x+4;
(3)如图3,∵PC为Rt△ACB的中线,
∴PC=AP=BP=BC=2,
∴△PCB为等边三角形,
∴∠BPN=∠BNP=30°,
∴PN=2$\sqrt{3}$,
过点A作AG⊥EF于G.
∴AG=$\frac{1}{2}$AC=$\sqrt{3}$,S△FCN=2S△AFC,
∵S△ACN=$\frac{1}{2}$×4×2$\sqrt{3}$=4$\sqrt{3}$,
∴S△FCN=$\frac{2}{3}$S△ACN=$\frac{2\sqrt{3}}{3}$=$\frac{1}{2}$×CF×2$\sqrt{3}$,CF=$\frac{2}{3}$,
∴PF=$\frac{2}{3}$.
点评 本题考查了几何变换综合题.涉及了等边直角三角形的判定与性质,全等三角形的判定与性质.综合考察的知识点较多,对于此类综合性较强的题目关键还是需要同学们有扎实的基本功注意培养自己的融会贯通能力.

 已知,等腰梯形ABCD中,AD∥BC,AC⊥BD,AD=3cm,BC=7cm,求梯形ABCD的面积.
已知,等腰梯形ABCD中,AD∥BC,AC⊥BD,AD=3cm,BC=7cm,求梯形ABCD的面积.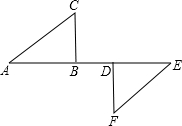 如图,点A,B,D,E在同一条直线上,AD=EB,BC∥DF,∠C=∠F,试判断△ABC与△EDF是否全等,并说明理由.
如图,点A,B,D,E在同一条直线上,AD=EB,BC∥DF,∠C=∠F,试判断△ABC与△EDF是否全等,并说明理由. 请在图中作出△ABC关于点O中心对称的图形.
请在图中作出△ABC关于点O中心对称的图形.