题目内容
9.已知点A在半径为3的⊙O内,OA等于1,点B是⊙O上一点,连接AB,当∠OBA取最大值时,AB的长度为2$\sqrt{2}$.分析 利用三角形的边角关系得到当∠OBA取最大值时,OA取最大值,则BA取最小值,于是判断BA⊥OA时,BA取最小值,然后利用勾股定理可计算此时AB的长.
解答 解:在△OBA中,当∠OBA取最大值时,OA取最大值,
∴BA取最小值,
又∵OA、OB是定值,
∴BA⊥OA时,BA取最小值;
在直角三角形OBA中,OA=1,OB=3,
∴AB=$\sqrt{{3}^{2}-{1}^{2}}$=2$\sqrt{2}$.
故答案为2$\sqrt{2}$.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目


 如图,在△ABC中,∠ABO=20°,∠ACO=25°,∠A=65°,则∠BOC的度数110°.
如图,在△ABC中,∠ABO=20°,∠ACO=25°,∠A=65°,则∠BOC的度数110°.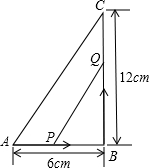 如图所示,在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果点P、Q分别从A、B同时出发.
如图所示,在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果点P、Q分别从A、B同时出发. △ABC内接于⊙O1,且∠C≥∠B,又⊙O2与⊙O1内切,且与AB、AC边均内切于切点M、N,求证:MN的中点即为△ABC的内心.
△ABC内接于⊙O1,且∠C≥∠B,又⊙O2与⊙O1内切,且与AB、AC边均内切于切点M、N,求证:MN的中点即为△ABC的内心.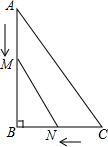 如图,在Rt△ABC中∠B=90°,AB=8m,BC=6m,点M、点N分别从A、C两点同时出发,分别沿AB、CB方向向点B匀速移动,它们的速度都是2m/s,问几秒后,△MBN的面积为Rt△ABC的面积的$\frac{1}{6}$?
如图,在Rt△ABC中∠B=90°,AB=8m,BC=6m,点M、点N分别从A、C两点同时出发,分别沿AB、CB方向向点B匀速移动,它们的速度都是2m/s,问几秒后,△MBN的面积为Rt△ABC的面积的$\frac{1}{6}$?