Question

1．△ABC内接于⊙O₁，且∠C≥∠B，又⊙O₂与⊙O₁内切，且与AB、AC边均内切于切点M、N，求证：MN的中点即为△ABC的内心．

Answer 1

分析 （1）作辅助线，构建直径及相似三角形，根据切线长定理得：AM=AN，且AO₂平分∠BAC；由等腰三角莆三线合一的性质可知：AO₂与MN的交点I是MN的中点，且AO₂是MN的中垂线；
（2）由相交弦定理得：O₂L•O₂T=O₂A•O₂E ①，与射影定理得：${O}_{2}{M}^{2}$=O₂I•O₂A ②，所以O₂M•TL=O₂A•EI  ③；
（3）证明△BEF∽△MO₂A，列式$\frac{EF}{{O}_{2}A}$=$\frac{BE}{M{O}_{2}}$，得EF•MO₂=O₂A•BE ④；
（4）③④结合得：BE=EI；
（5）由等边对等角得：∠EBI=∠EIB，根据外角定理和同弧所对的圆角周相等得：BI平分∠ABC，从而得出结论．

解答 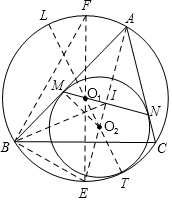证明：如图，作射线AO₂，交MN于I，交⊙O₁于E，设⊙O₁与⊙O₂的切点为T，作直径O₁O₂，交⊙O₁于L，则O₁、O₂、T共线，
∵AB、AC切⊙O₂于M、N两点，
∴AM=AN，∠BAO₂=∠CAO₂，
∴AO₂是MN的中垂线，
即I是MN的中点，
由相交弦定理得：O₂L•O₂T=O₂A•O₂E ①，
由O₂M⊥AB，O₂A⊥MN得：${O}_{2}{M}^{2}$=O₂I•O₂A ②，
∵O₂M=O₂T，
∴①+②得：O₂L•O₂T+${O}_{2}{M}^{2}$=O₂A•O₂E+O₂I•O₂A，
O₂M（O₂M+O₂L）=O₂A（O₂E+O₂I），
O₂M•TL=O₂A•EI  ③，
作⊙O₁的直径EF，连接BE、BF，
∴∠FBE=90°，
∴∠FBE=∠O₂MA=90°，
∵∠F=∠MAO₂，
∴△BEF∽△MO₂A，
∴$\frac{EF}{{O}_{2}A}$=$\frac{BE}{M{O}_{2}}$，
∴EF•MO₂=O₂A•BE ④，
∵EF=TL，
连接BI，
由③④得：O₂A•BE=O₂A•EI，
∴BE=EI，
∴∠EBI=∠EIB，
∵∠EIB=∠ABI+∠BAI，
∠EBI=∠EBC+∠IBC，
∵∠EBC=∠EAC=∠BAI，
∴∠ABI=∠IBC，
∴BI平分∠ABC，
∴I是△ABC的内心，且I是MN的中点，
∴MN的中点即为△ABC的内心．

点评 本题是曼海姆定理的证明，比较复杂，难度较大；考查了两圆内切、三角形的外接圆、内切圆等有关的性质，首先要明确内心是三角形三条角平分线的交点，知道切线长定理：圆外一点引圆的两条切线，切线长相等，这点与圆心的连线平分切线所成的夹角；同时还运用了直径所对的圆周角是直角及半径相等，两圆内切时，两圆的连心线过切点，熟练掌握与圆有关的性质是做好本题的关键．