题目内容
20. 如图,在平面直角坐标系中,点A在y轴上,坐标为(0,3),点B在x轴上.
如图,在平面直角坐标系中,点A在y轴上,坐标为(0,3),点B在x轴上.(1)在坐标系中求作一点M,使得点M到点A,点B和原点O这三点的距离相等,在图中保留作图痕迹,不写作法;
(2)若sin∠OAB=$\frac{4}{5}$,求点M的坐标.
分析 (1)直接利用线段垂直平分线的作法结合直角三角形的性质得出答案;
(2)利用勾股定理得出OB的长,再利用M点为AB的中点即可得出其坐标.
解答  解:(1)如图所示:点M,即为所求;
解:(1)如图所示:点M,即为所求;
(2)∵sin∠OAB=$\frac{4}{5}$,
∴设OB=4x,AB=5x,
由勾股定理可得:32+(4x)2=(5x)2,
解得:x=1,
由作图可得:M为AB的中点,则M的坐标为:(2,$\frac{3}{2}$).
点评 此题主要考查了基本作图以及线段垂直平分线的作法与性质,正确掌握线段垂直平分线的作法是解题关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
10. 如图所示的正方体,如果把它展开,可以得到( )
如图所示的正方体,如果把它展开,可以得到( )
 如图所示的正方体,如果把它展开,可以得到( )
如图所示的正方体,如果把它展开,可以得到( )| A. |  | B. |  | C. |  | D. |  |
10.下列说法中,正确的是( )
| A. | $\frac{5+2b}{a}$是多项式 | B. | -7πa2的系数是-7π | ||
| C. | 4x2y2-72x3+52是5次多项式 | D. | 单项式y的系数和次数都是零 |
7.已知点A(m,-2),点B(3,m-1),且直线AB∥x轴,则m的值为( )
| A. | -1 | B. | 1 | C. | -3 | D. | 3 |
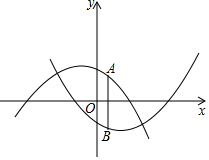 若我们规定二次函数y1=ax2+bx+c(α≠0)的″负相关函数″为y2=-ax2+bx-c.
若我们规定二次函数y1=ax2+bx+c(α≠0)的″负相关函数″为y2=-ax2+bx-c.
 如图,在长为6m,宽为4m的矩形地面上修建两条宽均为1m的道路,余下部分做为耕地,根据图中数据,计算耕地面积为15m2.
如图,在长为6m,宽为4m的矩形地面上修建两条宽均为1m的道路,余下部分做为耕地,根据图中数据,计算耕地面积为15m2.