Question

5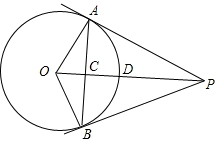．如图所示，PA，PB是⊙O的两条切线，A，B为切点，连接PO，交⊙O于点D，交AB于点C．
（1）写出圆中所有的垂直的关系；
（2）若PA=4，PD=2，求半径OA的长．

Answer 1

分析 （1）由PA，PB是⊙O的两条切线，根据切线的性质，即可证得OA⊥PA，OB⊥PB，又由切线长定理，可得AB⊥OP；
（2）首先设OA=x，然后由勾股定理得方程：x²+4²=（x+2）²，继而求得答案．

解答 解：（1）OA⊥PA，OB⊥PB，AB⊥OP；
理由：∵PA，PB是⊙O的两条切线，
∴OA⊥PA，OB⊥PB，PA=PB，∠APO=∠BPO，
∴AB⊥OP；

（2）设OA=x，则OP=OD+PD=x+2，
∵PA是切线，
∴OA⊥PA，
在Rt△OAP中，OA²+PA²=OP²，
即x²+4²=（x+2）²，
解得：x=3，
∴半径OA=3．

点评 此题考查了切线的性质、切线长定理以及勾股定理．注意掌握方程思想的应用是解此题的关键．