题目内容
20.解方程(1)(x-3)2+4x(x-3)=0(用适当法解)
(2)5(2x-1)=(1-2x)(x+3)(用因式分解法)
(3)$\frac{1}{2}$x(x-2)=x2-4x+4(用因式分解法)
(4)-$\frac{1}{2}$x2+ax+4a2=0(用配方法)
分析 (1)先把方程左边因式分解,求出x的值即可
(2)(3)先移项、再把方程左边因式分解,求出x的值即可;
(4)先把方程左边化为完全平方的形式,再用直接开方法求出x的值即可.
解答 解:(1)方程左边因式分解得,(x-3)(x-3+4x)=0,
故x-3=0或x-3+4x=0,
解得x1=3,x2=$\frac{3}{5}$;
(2)移项得,5(2x-1)+(2x-1)(x+3)=0,
方程左边因式分解得,(2x-1)(5+x+3)=0,
故2x-1=0或5+x+3=0,
解得x1=$\frac{1}{2}$,x2=-8;
(3)移项得,$\frac{1}{2}$x(x-2)-(x2-4x+4)=0,
方程左边因式分解得,(x-2)($\frac{1}{2}$x-x+2)=0,
故x-2=0或$\frac{1}{2}$x-x+2=0,
解得x1=2,x2=4;
(4)原方程可化为-$\frac{1}{2}$(x2-2ax+a2-a2)+4a2=0,即-$\frac{1}{2}$(x-a)2+$\frac{1}{2}$a2+4a2=0,
移项得,-$\frac{1}{2}$(x-a)2=-$\frac{9}{2}$a2,
方程两边同时乘以-2得,(x-a)2=9a2,
两边开方得,x-a=±3a,
故x1=4a,x2=-2a.
点评 本题考查的是解一元二次方程,熟知利用因式分解法解一元二次方程是解答此题的关键.

练习册系列答案
相关题目
11.已知A=5a-3b,B=-6a+4b,则A-B等于( )
| A. | -a+b | B. | 11a+b | C. | 11a-7b | D. | -a-7b |
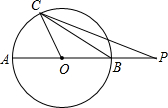 如图,AB是⊙O的直径,延长OB至P,使BP=OB,点C为圆上除A、B外的任一点.设∠PCB=α,∠POC=β.则tanα•tan$\frac{β}{2}$的值为$\frac{1}{3}$.
如图,AB是⊙O的直径,延长OB至P,使BP=OB,点C为圆上除A、B外的任一点.设∠PCB=α,∠POC=β.则tanα•tan$\frac{β}{2}$的值为$\frac{1}{3}$.