题目内容
池塘上悬着一盏灯A,在高出水面1米的地方B观测灯的仰角为20°,测得在塘中的像的俯角为30°,求此灯离水面的高度(观察时水面呈平静状态,
≈1.732,tan20°=0.3640,tan70°≈2.747,精确到0.1米)
| 3 |
考点:解直角三角形的应用-仰角俯角问题
专题:
分析:此题可设BE=x,则BC=x-1,B'C=x+1,在Rt△ABC和Rt△AB'C中,用∠B和∠B'的正切值表示出AC,则建立等式解出x的值即可.
解答: 解:如图,DE表示水面,A表示观测点,
解:如图,DE表示水面,A表示观测点,
B为灯的顶部,B'在水中的倒影,由题意:
∠BAC=20°,∠B'AC=30°,AD=1(m)∴∠B=70°,∠B'=60°,
设BE=x,则BC=x-1,B'C=x+1.
在Rt△ABC中,AC=BC•tanB=(x-1)tan70°
在Rt△AB'C中,AC=B'C•tanB'=(x+1)tan60°
(x-1)tan70°=(x+1)tan60°,
∴(tan70°-tan60°)x=tan70°+tan60°1.015x=4.479,
∴x≈4.41米.
答:此灯离水面的高度为4.41米.
 解:如图,DE表示水面,A表示观测点,
解:如图,DE表示水面,A表示观测点,B为灯的顶部,B'在水中的倒影,由题意:
∠BAC=20°,∠B'AC=30°,AD=1(m)∴∠B=70°,∠B'=60°,
设BE=x,则BC=x-1,B'C=x+1.
在Rt△ABC中,AC=BC•tanB=(x-1)tan70°
在Rt△AB'C中,AC=B'C•tanB'=(x+1)tan60°
(x-1)tan70°=(x+1)tan60°,
∴(tan70°-tan60°)x=tan70°+tan60°1.015x=4.479,
∴x≈4.41米.
答:此灯离水面的高度为4.41米.
点评:本题考查俯仰角的定义,要求学生能借助俯仰角构造直角三角形并解直角三角形.

练习册系列答案
相关题目
下列说法正确的是( )
| A、对角线相等且互相平分的四边形是菱形 |
| B、对角线相等且互相垂直的四边形是菱形 |
| C、对角线相等且互相平分的四边形是矩形 |
| D、对角线相等且垂直的四边形是正方形 |
 如图,三个皮带轮的半径都是10dm,中心距离BC=30dm,AC=40dm,AB=50dm,求皮带的长度.
如图,三个皮带轮的半径都是10dm,中心距离BC=30dm,AC=40dm,AB=50dm,求皮带的长度.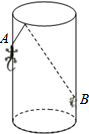 如图,圆柱形容器中,高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,求壁虎捕捉蚊子的最短距离.(容器厚度忽略不计)
如图,圆柱形容器中,高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,求壁虎捕捉蚊子的最短距离.(容器厚度忽略不计)