Question

18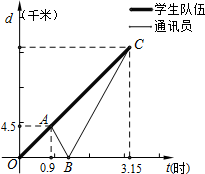．一队学生从学校出发去劳动基地军训，行进的路程与时间的图象如图所示，队伍走了0.9小时后，队伍中的通讯员按原路加快速度返回学校拿材料，通讯员经过0.5小时后回到学校，然后随即按原来加快的速度追赶队伍，恰好在劳动基地追上学生队伍．设学生队伍与学校的距离为d₁，通讯员与学校的距离为d₂，试根据图象解决下列问题：
（1）填空：学生队伍的行进速度v=5千米/小时；
（2）当0.9≤t≤3.15时，求d₂与t的函数关系式；
（3）已知学生队伍与通讯员的距离不超过3千米时，能用无线对讲机保持联系，试求在上述过程中通讯员离开队伍后他们能用无线对讲机保持联系时t的取值范围．

Answer 1

分析 （1）根据函数图象可得：当t=0.9h时，学生队伍走的路程s=4.5km，即可解答；
（2）通讯员经过0.5小时后回到学校，0.9+0.5=1.4，所以B点的坐标为（1.4，0），当0.9≤t≤3.15时，分别求线段AB和线段BC的解析式，即可解答；
（3）求出线段OC的解析式，分两种情况进行讨论即可解答．

解答 解：（1）根据函数图象可得：当t=0.9h时，学生队伍走的路程s=4.5km，
∴学生队伍行进的速度为：4.5÷0.9=5（km/h），
故答案为：5．

（2）∵通讯员经过0.5小时后回到学校，0.9+0.5=1.4，∴B点的坐标为（1.4，0）
设线段AB的解析式为：d₂=kt+b（k≠0），（0.9≤t≤1.4），
又过点A（0.9，4.5）、B（1.4，0），
∴$\left\{\begin{array}{l}{0.9k+b=4.5}\\{1.4k+b=0}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=-9}\\{b=12.6}\end{array}\right.$，
∴线段AB的解析式为：d₂=-9t+12.6，（0.9≤t≤1.4）．
∵通讯员按原来的速度随即追赶队伍，∴速度为4.5÷0.5=9千米/小时．
设线段BC的解析式为：d₂=9t+m，（1.4≤t≤3.15），
又过点B（1.4，0），
∴0=9×1.4+m，
解得：m=-12.6，
∴线段BC的解析式为：d₂=9t-12.6，（1.4≤t≤3.15），
∴${d}_{2}=\left\{\begin{array}{l}{-9t+12.6（0.9≤t≤1.4）}\\{9t-12.6（1.4＜t≤3.15）}\end{array}\right.$．

（3）设线段OC的解析式为：d₁=nt（n≠0），又过点A（0.9，4.5），
∴4.5N=0.9，
∴n=5．
∴线段OC的解析式为：d₁=5t，
设时间为t小时，学生队伍与通讯员相距不超过3千米，下面分两种情况讨论：
①当0.9≤t≤1.4时，d₁-d₂≤3，即5t-（-9t+12.6）≤3，
解得：$t≤\frac{39}{35}$，
∴$0.9＜t≤\frac{39}{35}$．
②当1.4≤t≤3.15时，d₁-d₂≤3即5t-（9t-12.6）≤3，
解得：t≥2.4，
∴2.4≤t≤3.15．
故通讯员离开队伍后他们能用无线对讲机保持联系时t的取值范围为$0.9＜t≤\frac{39}{35}$
或2.4≤t≤3.15．

点评 本题考查了一次函数的应用，解决本题的关键是分类讨论思想的应用．