题目内容
14. 如图(1),AB∥CD,猜想∠BPD与∠B、∠D的关系,说明理由.
如图(1),AB∥CD,猜想∠BPD与∠B、∠D的关系,说明理由.(提示:三角形的内角和等于180°)
①填空或填写理由
解:猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180°两直线平行,同旁内角互补
∵AB∥CD,EF∥AB,
∴CD∥EF,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠EPD+∠CDP=180°
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
②依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B、∠D的关系,并说明理由.
③观察图(3)和(4),已知AB∥CD,直接写出图中的∠BPD与∠B、∠D的关系,不说明理由.
分析 ①过点P作EF∥AB,根据两直线平行,同旁内角互补,证出结论;
②与①的方法类似,过点P作EP∥AB,根据两直线平行,内错角相等,证出结论;
③过点P作EP∥AB,可以看出图中的∠BPD与∠B、∠D的关系.
解答 解:①猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180°(两直线平行,同旁内角互补)
∵AB∥CD,EF∥AB,
∴CD∥EF,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠EPD+∠CDP=180°
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
②猜想∠BPD=∠B+∠D
理由:过点P作EP∥AB,
∴∠B=∠BPE(两直线平行,同位角相等)
∵AB∥CD,EF∥AB,
∴CD∥EF,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠EPD=∠D
∴∠BPD=∠B+∠D
③与②的作法相同,过点P作EP∥AB
(3)∠BPD+∠B=∠D,(4)∠BPD=∠B-∠D
点评 本题考查的是平行线的性质,作出正确的辅助线是解题的关键,解答本题时,注意类比思想的运用.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
9.某品牌折扣店将某件衣服按进价提高50%后标价,再打八折销售,获利40元.设这件的进价为x元,根据题意,下面所列方程正确的是( )
| A. | x•50%×80%-x=40 | B. | x(1+50%)×80%-x=40 | ||
| C. | (x+50%)•80%-x=40 | D. | x(1+50%)(1-20%)-x=40 |
6.若等腰三角形的两边长是8和3,则此三角形的周长是( )
| A. | 19 | B. | 14 | C. | 19或14 | D. | 不能确定 |
3.能使两个直角三角形全等的条件是( )
| A. | 两条边对应相等 | B. | 一条边对应相等 | C. | 一锐角对应相等 | D. | 两锐角对应相等 |
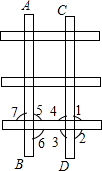 如图,在铺设铁轨时,两条铁轨必须是平行的,已知∠1是直角,那么再测量图中的哪个角(仅限图中已标出的角),就可以判断图中的两条铁轨AB、CD是否平行?为什么.
如图,在铺设铁轨时,两条铁轨必须是平行的,已知∠1是直角,那么再测量图中的哪个角(仅限图中已标出的角),就可以判断图中的两条铁轨AB、CD是否平行?为什么. 如图是一个正方形及其内切圆,随机地往正方形内投一粒米,落在圆内的概率为$\frac{π}{4}$.
如图是一个正方形及其内切圆,随机地往正方形内投一粒米,落在圆内的概率为$\frac{π}{4}$. A、B两种商品在一段时间内的销售总量如图所示:
A、B两种商品在一段时间内的销售总量如图所示: