ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΈ Χβ‘Όœ÷ΘΚ
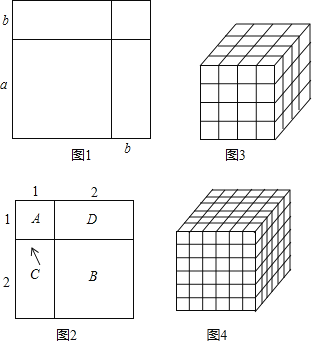
ΐ–ΈΫαΚœ «ΫβΨω ΐ―ßΈ ΧβΒΡ“Μ÷÷÷Ί“ΣΒΡΥΦœκΖΫΖ®Θ§Ϋη÷ζ’β÷÷ΖΫΖ®Ω…ΫΪ≥ιœσΒΡ ΐ―ß÷Σ Ε±δΒΟ÷±ΙέΤπά¥≤Δ«“ΨΏ”–Ω…≤ΌΉς–‘Θ§¥”ΕχΩ…“‘Αο÷ζΈ“Ο«ΩλΥΌΫβΧβΘ°≥θ÷– ΐ―ßάοΒΡ“Μ–©¥ζ ΐΙΪ ΫΘ§ΚήΕύΕΦΩ…“‘Ά®Ιΐ±μ ΨΦΗΚΈΆΦ–ΈΟφΜΐΒΡΖΫΖ®Ϋχ––÷±ΙέΆΤΒΦΚΆΫβ ΆΘ°άΐ»γΘΚάϊ”ΟΆΦ–ΈΒΡΦΗΚΈ“β“εΆΤ÷ΛΆξ»ΪΤΫΖΫΙΪ ΫΘ°ΫΪ“ΜΗω±Ώ≥ΛΈΣaΒΡ’ΐΖΫ–ΈΒΡ±Ώ≥Λ‘ωΦ”bΘ§–Έ≥…ΝΫΗωΨΊ–ΈΚΆΝΫΗω’ΐΖΫ–ΈΘ§»γΆΦ1Θ§’βΗωΆΦ–ΈΒΡΟφΜΐΩ…“‘±μ Ψ≥…ΘΚΘ®a+bΘ©2Μρa2+2ab+b2ΓύΘ®a+bΘ©2ΘΫa2+2ab+b2
’βΨΆ―ι÷ΛΝΥΝΫ ΐΚΆΒΡΆξ»ΪΤΫΖΫΙΪ ΫΘ°
Έ ΧβΧα≥ωΘΚ
»γΚΈάϊ”ΟΆΦ–ΈΦΗΚΈ“β“εΒΡΖΫΖ®ΆΤ÷ΛΘΚ13+23ΘΫ32 »γΆΦ2Θ§A±μ Ψ1Ηω1ΓΝ1ΒΡ’ΐΖΫ–ΈΘ§Φ¥ΘΚ1ΓΝ1ΓΝ1ΘΫ13Θ§B±μ Ψ1Ηω2ΓΝ2ΒΡ’ΐΖΫ–ΈΘ§C”κD«ΓΚΟΩ…“‘Τ¥≥…1Ηω2ΓΝ2ΒΡ’ΐΖΫ–ΈΘ§“ρ¥ΥΘΚBΓΔCΓΔDΨΆΩ…“‘±μ Ψ2Ηω2ΓΝ2ΒΡ’ΐΖΫ–ΈΘ§Φ¥ΘΚ2ΓΝ2ΓΝ2ΘΫ23Θ§ΕχAΓΔBΓΔCΓΔD«ΓΚΟΩ…“‘Τ¥≥…“ΜΗωΘ®1+2Θ©ΓΝΘ®1+2Θ©ΒΡ¥σ’ΐΖΫ–ΈΘ§”…¥ΥΩ…ΒΟΘΚ13+23ΘΫΘ®1+2Θ©2ΘΫ32
≥Δ ‘ΫβΨωΘΚ
«κΡψάύ±»…œ ωΆΤΒΦΙΐ≥ΧΘ§άϊ”ΟΆΦ–ΈΦΗΚΈ“β“εΖΫΖ®ΆΤ÷ΛΘΚ13+23+33ΘΫΓΓ ΓΓΘ®“Σ«σΉ‘ΦΚΙΙ‘λΆΦ–Έ≤Δ–¥≥ωΆΤ÷ΛΙΐ≥ΧΘ©
άύ±»ΙιΡ…ΘΚ
«κ”Ο…œΟφΒΡ±μ ΨΦΗΚΈΆΦ–ΈΟφΜΐΒΡΖΫΖ®ΧΫΨΩΘΚ13+23+33+Γ≠+n3ΘΫΓΓ ΓΓΘ®“Σ«σ÷±Ϋ”–¥≥ωΫα¬έΘ§≤Μ±Ί–¥≥ωΫβΧβΙΐ≥ΧΘ©
ΒΦ ”Π”ΟΘΚ
ΆΦ3 «”…άβ≥ΛΈΣ1ΒΡ–Γ’ΐΖΫΧε¥ν≥…ΒΡ¥σ’ΐΖΫΧεΘ§ΆΦ÷–¥σ–Γ’ΐΖΫΧε“ΜΙ≤”–Εύ…ΌΗωΘΩΈΣΝΥ’ΐ»Ζ ΐ≥ω¥σ–Γ’ΐΖΫΧεΒΡΉήΗω ΐΘ§Έ“Ο«Ω…“‘Ζ÷άύΆ≥ΦΤΘ§Φ¥Ζ÷±π ΐ≥ωάβ≥Λ «1Θ§2Θ§3ΚΆ4ΒΡ’ΐΖΫΧεΒΡΗω ΐΘ§‘Ό«σΉήΚΆΘ°
άΐ»γΘΚάβ≥Λ «1ΒΡ’ΐΖΫΧε”–ΘΚ4ΓΝ4ΓΝ4ΘΫ43ΗωΘ§άβ≥Λ «2ΒΡ’ΐΖΫΧε”–ΘΚ3ΓΝ3ΓΝ3ΘΫ33ΗωΘ§άβ≥Λ «3ΒΡ’ΐΖΫΧε”–ΘΚ2ΓΝ2ΓΝ2ΘΫ23ΗωΘ§άβ≥Λ «4ΒΡ’ΐΖΫΧε”–ΘΚ1ΓΝ1ΓΝlΘΫ13ΗωΘ§»ΜΚσάϊ”ΟΘ®3Θ©άύ±»ΙιΡ…ΒΡΫα¬έΘ§Ω…ΒΟΘΚΓΓΓΓΘΫΓΓ ΓΓΆΦ4 «”…άβ≥ΛΈΣ1ΒΡ–Γ’ΐΖΫΧε≥…ΒΡ¥σ’ΐΖΫΧεΘ§ΆΦ÷–¥σ–Γ’ΐΖΫΧε“ΜΙ≤”–ΓΓ ΓΓΗωΘ°
Ρφœρ”Π”ΟΘΚ
»γΙϊ”…άβ≥ΛΈΣ1ΒΡ–Γ’ΐΖΫΧε¥ν≥…ΒΡ¥σ’ΐΖΫΧε÷–Θ§Ά®Ιΐ…œΟφΒΡΖΫ Ϋ ΐ≥ωΒΡ¥σ–Γ’ΐΖΫΧε“ΜΙ≤”–44100ΗωΘ§Ρ«Ο¥άβ≥ΛΈΣ1ΒΡ–Γ’ΐΖΫΧε“ΜΙ≤”–ΓΓ ΓΓΗωΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©Θ®1+2+3Θ©2ΘΜΘ®2Θ©Θ®1+2+3+Γ≠+nΘ©2ΘΜΘ®3Θ©13+23+33+43Θ§Θ®1+2+3+4Θ©2Θ§100ΗωΘΜΘ®4Θ©8000Θ°
ΓΨΫβΈωΓΩ
ΗυΨίΙφ¬…Ω…“‘άϊ”ΟœύΆ§ΒΡΖΫΖ®Ϋχ––ΧΫΨΩΆΤ÷ΛΘ§”…”Ύ «ΧΫΨΩ13+23+33ΘΫΘΩΩœΕ®ΙΙ≥…¥σ’ΐΖΫ–Έ”–9ΗωΜυ±ΨΆΦ–ΈΘ®3Ηω’ΐΖΫ–Έ6Ηω≥ΛΖΫ–ΈΘ©Ήι≥…Θ§»γΆΦΥυ ΨΩ…“‘ΆΤ÷ΛΘ°
ΒΦ ”Π”ΟΘΚΗυΨίΙφ¬…«σ¥σ’ΐΖΫΧε÷–Κ§”–Εύ…ΌΗω’ΐΖΫΧεΘ§Ω…“‘ΉΣΜ·ΈΣ13+23+33+Γ≠+n3ΘΫΘ®1+2+3+Γ≠+nΘ©2ά¥«σΒΟΘ°
Ρφœρ”Π”ΟΘΚΩ…ΫΪΉήΗω ΐΩ¥≥…m2Θ§»ΜΚσ‘Ό–¥≥…ΘΫΘ®1+2+3+Γ≠+nΘ©2ΒΟ≥ω¥σ’ΐΖΫ–ΈΟΩΧθ±Ώ…œ”–ΦΗΗωάβ≥ΛΈΣ1ΒΡ–Γ’ΐΖΫΧεΘ§ΫχΕχΦΤΥψ≥ωάβ≥ΛΈΣ1ΒΡ–Γ’ΐΖΫΧεΒΡΗω ΐΘ°
ΫβΘΚ»γΆΦΘ§A±μ Ψ1Ηω1ΓΝ1ΒΡ’ΐΖΫ–ΈΘ§Φ¥1ΓΝ1ΓΝ1ΘΫ13ΘΜ
B±μ Ψ1Ηω2ΓΝ2ΒΡ’ΐΖΫ–ΈΘ§C”κD«ΓΚΟΩ…“‘Τ¥≥…1Ηω2ΓΝ2ΒΡ’ΐΖΫ–ΈΘ§
“ρ¥ΥBΓΔCΓΔDΨΆΩ…“‘Τ¥≥…2Ηω2ΓΝ2ΒΡ’ΐΖΫ–ΈΘ§Φ¥ΘΚ2ΓΝ2ΓΝ2ΘΫ23ΘΜ
G”κHΓΔE”κFΚΆΩ…“‘Τ¥≥…3Ηω3ΓΝ3ΒΡ’ΐΖΫ–ΈΘ§Φ¥ΘΚ3ΓΝ3ΓΝ3ΘΫ33ΘΜ
Εχ’ϊΗωΆΦ–Έ«ΓΚΟΩ…“‘Τ¥≥…“ΜΗωΘ®1+2+3Θ©ΓΝΘ®1+2+3Θ©ΒΡ¥σ’ΐΖΫ–ΈΘ§
“ρ¥ΥΩ…ΒΟΘΚ13+23+33ΘΫΘ®1+2+3Θ©2ΘΫ62Θ°
Ι ¥πΑΗΈΣΘΚΘ®1+2+3Θ©2Μρ62Θ°
ΗυΨίΙφ¬…Ω…ΒΟΘΚ13+23+33+Γ≠+n3ΘΫΘ®1+2+3+Γ≠+nΘ©2Θ°
“άΨίΙφ¬…ΒΟΘΚ13+23+33+43ΘΫΘ®1+2+3+4Θ©2ΘΫ102ΘΫ100Θ°
Ι ¥πΑΗΈΣΘΚ13+23+33+43ΘΫΘ®1+2+3+4Θ©2 100
ΓΏ44100ΘΫ2102ΘΫΘ®1+2+3+Γ≠+nΘ©2
ΓύnΘΫ20
Γύ20ΓΝ20ΓΝ20ΘΫ8000
Ι ¥πΑΗΈΣ8000Θ°

ΓΨΧβΡΩΓΩΈΣΝΥΗχ”ΈΩΆΧαΙ©ΗϋΚΟΒΡΖΰΈώΘ§Ρ≥ΨΑ«χΥφΜζΕ‘≤ΩΖ÷”ΈΩΆΫχ––ΝΥΙΊ”ΎΓΑΨΑ«χΖΰΈώΙΛΉς¬ζ“βΕ»Γ±ΒΡΒς≤ιΘ§≤ΔΗυΨίΒς≤ιΫαΙϊΜφ÷Τ≥…»γœ¬≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦ±μ.
¬ζ“βΕ» | »Υ ΐ | Υυ’ΦΑΌΖ÷±» |
Ζ«≥Θ¬ζ“β | 12 | 10% |
¬ζ“β | 54 | m |
±»Ϋœ¬ζ“β | n | 40% |
≤Μ¬ζ“β | 6 | 5% |
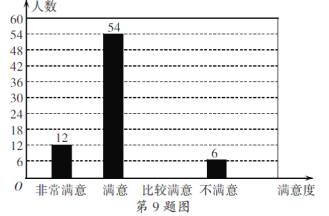
ΗυΨίΆΦ±μ–≈œΔΘ§Ϋβ¥πœ¬Ν–Έ ΧβΘΚ
(1)±Ψ¥ΈΒς≤ιΒΡΉή»Υ ΐΈΣ______Θ§±μ÷–mΒΡ÷ΒΈΣ_______ΘΜ
(2)«κ≤Ι»ΪΧθ–ΈΆ≥ΦΤΆΦΘΜ
(3)ΨίΆ≥ΦΤΘ§ΗΟΨΑ«χΤΫΨυΟΩΧλΫ”¥ΐ”ΈΩΆ‘Φ3600»ΥΘ§»τΫΪΓΑΖ«≥Θ¬ζ“βΓ±ΚΆΓΑ¬ζ“βΓ±ΉςΈΣ”ΈΩΆΕ‘ΨΑ«χΖΰΈώΙΛΉςΒΡΩœΕ®Θ§«κΡψΙάΦΤΗΟΨΑ«χΖΰΈώΙΛΉςΤΫΨυΟΩΧλΒΟΒΫΕύ…ΌΟϊ”ΈΩΆΒΡΩœΕ®.
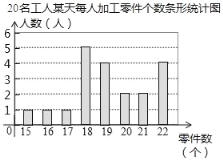
ΓΨΧβΡΩΓΩΡ≥≤ΩΟ≈ΈΣΝΥΫβΙΛ»ΥΒΡ…ζ≤ζΡήΝΠ«ιΩωΘ§Ϋχ––ΝΥ≥ι―υΒς≤ιΘ°ΗΟ≤ΩΟ≈ΥφΜζ≥ι»ΓΝΥ20ΟϊΙΛ»ΥΡ≥ΧλΟΩ»ΥΦ”ΙΛΝψΦΰΒΡΗω ΐΘ§ ΐΨί»γœ¬ΘΚ’ϊάμ…œΟφ ΐΨίΘ§ΒΟΒΫΧθ–ΈΆ≥ΦΤΆΦΘΜ―υ±Ψ ΐΨίΒΡΤΫΨυ ΐΓΔ÷Ύ ΐΓΔ÷–ΈΜ ΐ»γ±μΥυ ΨΘΚ
Ά≥ΦΤΝΩ | ΤΫΨυ ΐ | ÷Ύ ΐ | ÷–ΈΜ ΐ |
ΐ÷Β | 19.2 | m | n |
ΗυΨί“‘…œ–≈œΔΘ§Ϋβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©…œ±μ÷–mΓΔnΒΡ÷ΒΖ÷±πΈΣΓΓ ΓΓΘ§ΓΓ ΓΓΘΜ
Θ®2Θ©ΈΣΒςΕ·ΜΐΦΪ–‘Θ§ΗΟ≤ΩΟ≈ΗυΨίΙΛ»ΥΟΩΧλΦ”ΙΛΝψΦΰΒΡΗω ΐ÷ΤΕ®ΝΥΫ±άχ±ξΉΦΘ§Ζ≤¥οΒΫΜρ≥§Ιΐ’βΗω±ξΉΦΒΡΙΛ»ΥΫΪΜώΒΟΫ±άχΘ°»γΙϊœκ»Ο60%Ήσ”“ΒΡΙΛ»ΥΡήΜώΫ±Θ§”ΠΗυΨίΓΓ ΓΓά¥»ΖΕ®Ϋ±άχ±ξΉΦ±»ΫœΚœ Θ®ΧνΓΑΤΫΨυ ΐΓ±ΓΔΓΑ÷Ύ ΐΓ±ΜρΓΑ÷–ΈΜ ΐΓ±Θ©ΘΜ
Θ®3Θ©ΗΟ≤ΩΟ≈ΙφΕ®ΘΚΟΩΧλΦ”ΙΛΝψΦΰΒΡΗω ΐ¥οΒΫΜρ≥§Ιΐ21ΗωΒΡΙΛ»ΥΈΣ…ζ≤ζΡή ÷»τΗΟ≤ΩΟ≈”–300ΟϊΙΛ»ΥΘ§ ‘ΙάΦΤΗΟ≤ΩΟ≈…ζ≤ζΡή ÷ΒΡ»Υ ΐΘΜ
Θ®4Θ©œ÷ΨωΕ®¥”–ΓΆθΓΔ–Γ’≈ΓΔ–ΓάνΓΔ–ΓΝθ÷–―ΓΝΫ»Υ≤ΈΦ”“ΒΈώΡή ÷±»»ϋΘ§÷±Ϋ”–¥≥ω«ΓΚΟ―Γ÷––Γ’≈ΓΔ–ΓάνΝΫ»ΥΒΡΗ≈¬ Θ°