题目内容
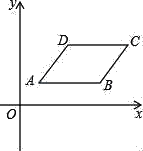
【题目】平面内,如图,在□ABCD中,AB=10,AD=15,![]() ,点P为AD边上任意点,连接PB,将PB绕点P逆时针旋转90°得到线段PQ.
,点P为AD边上任意点,连接PB,将PB绕点P逆时针旋转90°得到线段PQ.
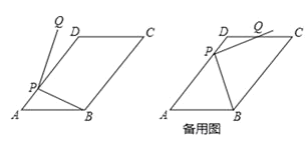
(1)当∠DPQ= 10°时,求∠APB的大小;
(2)当 ![]() 时,求点Q与点B间的距离(结果保留根号);
时,求点Q与点B间的距离(结果保留根号);
(3)若点Q恰好落在口ABCD的边所在的直线上,直接写出PB旋转到PQ所扫过的面积.(结果保留π).
【答案】(1)当∠DPQ=10°时,∠APB的值为80°或100°;(2)![]() ;(3)PB旋转到PQ所扫过的面积为32π或20π或16π.
;(3)PB旋转到PQ所扫过的面积为32π或20π或16π.
【解析】
(1)根据题意画出图形分情况讨论:①当点Q在平行四边形ABCD内时,②当点Q在平行四边形ABCD外时,结合题意分别求得答案.
(2) 连接BQ,作PE⊥AB于E,由已知结合题意即可求得tan∠ABP=2,在Rt△APE中,根据正切函数定义可设PE=4k,则AE=3k,在Rt△PBE中,根据正切函数定义可得EB=2k,
由AB=AE+EB即可求得k值,从而可得PE=8,EB=4,在Rt△PBE中,根据勾股定理可求得PB长,由等腰直角三角形性质可求得BQ长 .
(3)分三种情形分别求解即可; ①如图,当点Q落在直线BC上时,作BE⊥AD于E,PF⊥BC于F;在Rt△AEB中,根据正切tanA的值可求得BE=8,AE=6,从而可得PF=BE=8,根据等腰直角三角形的性质可得PF=BF=FQ=8,根据勾股定理可得PB=PQ=![]() ,根据扇形面积公式可得PB旋转到PQ所扫过的面积;
,根据扇形面积公式可得PB旋转到PQ所扫过的面积;
②如图,当点Q落在CD上时,作BE⊥AD于E,QF⊥AD交AD的延长线于F;设PE=x,由全等三角形判定可得△PBE≌△QPF,再由正切函数定义列方程可求PE=4,在Rt△PEB中,根据勾股定理求得PB=4![]() ,根据扇形面积公式可得PB旋转到PQ所扫过的面积;
,根据扇形面积公式可得PB旋转到PQ所扫过的面积;
③如图,当点Q落在AD上时,易知PB=PQ=8,根据扇形面积公式可得PB旋转到PQ所扫过的面积.
(1)解:如图1中,
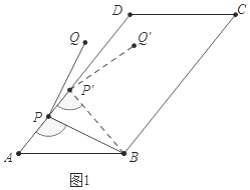
①当点Q在平行四边形ABCD内时,∠AP′B=180°∠Q′P′B∠Q′P′D=180°90°10°=80°
②当点Q在平行四边形ABCD外时,∠APB=180°(∠QPB∠QPD)=180°(90°10°)=100°
综上所述,当∠DPQ=10°时,∠APB的值为80°或100°
(2)如图2中,连接BQ,作PE⊥AB于E.
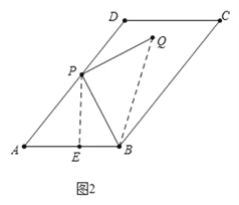
∵tan∠ABP:tanA=3:2,tanA=![]() ,
,
∴tan∠ABP=2,在Rt△APE中,tanA=![]() ,
,
设PE=4k,则AE=3k,在Rt△PBE中,tan∠ABP=![]() =2,
=2,
∴EB=2k,
∴AB=5k=10,
∴k=2,
∴PE=8,EB=4,
∴PB=![]() ,
,
∵△BPQ是等腰直角三角形,
∴BQ=![]() PB=
PB= ![]() .
.
(3)①如图3中,当点Q落在直线BC上时,作BE⊥AD于E,PF⊥BC于F. 则四边形BEPF是矩形。
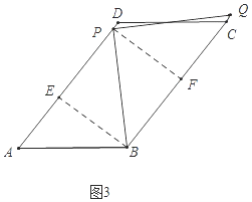
在Rt△AEB中,∵tanA=![]() ,
,
∵AB=10,∴BE=8,AE=6,
∴PF=BE=8,
∵△BPQ是等腰直角三角形,PF⊥BQ,∴PF=BF=FQ=8,
∴PB=PQ=![]() ,
,
∴PB旋转到PQ所扫过的面积=![]() .
.
②如图4中,当点Q落在CD上时,作BE⊥AD于E,QF⊥AD交AD的延长线于F. 设PE=x.
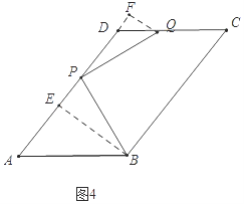
易证△PBE≌△QPF,
∴PE=QF=x,EB=PF=8,∴DF=AE+PE+PFAD=x1,∵CD∥AB,∴∠FDQ=∠A,
∴tan∠FDQ=tanA=![]() ,
,
∴![]() ,
,
∴x=4,∴PE=4,
在Rt△PEB中,PB= ![]() ,
,
∴PB旋转到PQ所扫过的面积=![]() .
.
③如图5中,
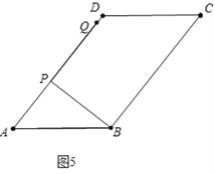
当点Q落在AD上时,易知PB=PQ=8,
∴PB旋转到PQ所扫过的面积=![]() ,
,
综上所述,PB旋转到PQ所扫过的面积为32π或20π或16π.