题目内容
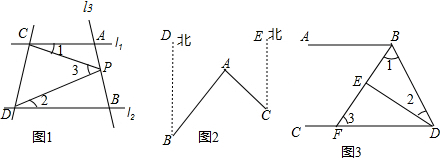
9.(1)如图1,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在线段AB上,则∠1,∠2,∠3之间的等量关系是∠3=∠1+∠2;如图2,点A在B处北偏东40°方向,在C处的北偏西45°方向,则∠BAC=85°.(2)如图3,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°,试说明:AB∥CD;并探究∠2与∠3的数量关系.
分析 (1)在图1中,作PM∥AC,利用平行线性质即可证明;利用①结论即可求得∠BAC的度数.
(2)根据BE、DE平分∠ABD、∠BDC,且∠1+∠2=90°,可得∠ABD+∠BDC=180°,根据同旁内角互补,可得两直线平行.根据∠1+∠2=90°,即∠BED=90°;那么∠3+∠FDE=90°,将等角代换,即可得出∠3与∠2的数量关系.
解答 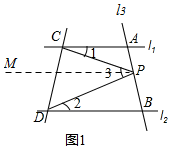 解:(1)如图1中,作PM∥AC,
解:(1)如图1中,作PM∥AC,
∵AC∥BD,
∴PM∥BD,
∴∠1=∠CPM,∠2=∠MPD,
∴∠1+∠2=∠CPM+∠MPD=∠CPD=∠3.
由题可知:∠BAC=∠B+∠C,
∵∠B=40°,∠C=45°,
∴∠BAC=40°+45°=85°.
故答案为:∠1+∠2=∠3,85°.
(2)证明:∵BE、DE平分∠ABD、∠BDC,
∴∠1=$\frac{1}{2}$∠ABD,∠2=$\frac{1}{2}$∠BDC;
∵∠1+∠2=90°,
∴∠ABD+∠BDC=180°;
∴AB∥CD;(同旁内角互补,两直线平行)
∵DE平分∠BDC,
∴∠2=∠FDE;
∵∠1+∠2=90°,
∴∠BED=∠DEF=90°;
∴∠3+∠FDE=90°;
∴∠2+∠3=90°.
点评 此题主要考查了角平分线的性质以及平行线的判定,正确添加辅助线是解决问题的关键.

练习册系列答案
相关题目
19.已知四边形ABCD是平行四边形,下列结论中不正确的是( )
| A. | 当AB=BC时,它是菱形 | B. | 当AC⊥BD时,它是菱形 | ||
| C. | 当∠ABC=90°时,它是矩形 | D. | 当AC=BD时,它是正方形 |
20.若直线y=3x+m经过第一、三、四象限,则抛物线y=(x-m)2+1的顶点在第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
17.如果某河的水位升高0.6米,水位变化记作+0.6米;那么水位下降0.2米时,水位变化记作( )
| A. | 0米 | B. | 0.2米 | C. | -0.8米 | D. | -0.2米 |
14.在下列调查中,宜采用全面调查的是( )
| A. | 了解某区中小学生视力情况 | B. | 了解七(2)班学生校服的尺码情况 | ||
| C. | 检测一批炮弹的使用寿命 | D. | 调查《1818黄金眼》栏目的收视率 |
1. 如图,在△ABC中,AC=6,BC=4,AB的垂直平分线交AC于点D,则△BDC的周长是( )
如图,在△ABC中,AC=6,BC=4,AB的垂直平分线交AC于点D,则△BDC的周长是( )
 如图,在△ABC中,AC=6,BC=4,AB的垂直平分线交AC于点D,则△BDC的周长是( )
如图,在△ABC中,AC=6,BC=4,AB的垂直平分线交AC于点D,则△BDC的周长是( )| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
18.图中,不是正方体的展开图是( )
| A. |  | B. |  | C. |  | D. |  |