计算 (1)$\sqrt{45}$+$\sqrt{108}$+$\sqrt{1\frac{1}{3}}$-$\sqrt{125}$-2．题目和参考答案——青夏教育精英家教网—

题目内容

1．计算
（1）$\sqrt{45}$+$\sqrt{108}$+$\sqrt{1\frac{1}{3}}$-$\sqrt{125}$
（2）（7+4$\sqrt{3}$）（7-4$\sqrt{3}$）-（3$\sqrt{5}$-1）²．

分析（1）先把各二次根式化为最简二次根式，然后合并即可；
（2）利用平方差公式和完全平方公式计算．

解答解：（1）原式=3$\sqrt{5}$+6$\sqrt{3}$+$\frac{2\sqrt{3}}{3}$-5$\sqrt{5}$
=$\frac{20\sqrt{3}}{3}$-2$\sqrt{5}$；
（2）原式=49-48-（45-6$\sqrt{5}$+1）
=1-46+6$\sqrt{5}$
=-45+6$\sqrt{5}$．

点评本题考查了二次根式的计算：先把各二次根式化为最简二次根式，再进行二次根式的乘除运算，然后合并同类二次根式．

练习册系列答案

随堂新卷系列答案

堂堂清课堂8分钟小测系列答案

特级教师小学毕业升学系统总复习系列答案

12．在矩形ABCD中，AB=a，AD=8．
（1）填空：矩形ABCD的面积为8a；（用含a的代数式表示）
（2）将矩形ABCD折叠，使得顶点B落在CD边上的P点处（如图1），折痕与边bc交与点O，连结AP、OP、OA．求证：△OCP∽△PDA；
（3）在（2）的条件下，若△OCP与△PDA的面积比为1：4．
①求a的值；
②擦去AO、OP，；连结BP（如图2）．动点M在线段AP上（与p、A）不重合），动点N在线段AB的延长线上，且BN=PM，连结MN交PB于点F，作ME⊥BP于点E．试问当点M、N在移动过程中，线段EF的长度是否发生变化？若变化，说明理由；若不变，求出线段EF的长度．

9．（7ab+2）²．

16．在以下实数：-$\sqrt{2}$，$\sqrt{16}$，π，3.1416，（$\sqrt{3}$）²，$\frac{22}{7}$，0.15，0.020020002…（每两个2之间零的个数依次增加1）中，无理数有（　　）个．

6．

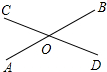如图，直线AB与CD相交于点O，若∠AOC=$\frac{1}{3}$∠AOD，则∠BOD的度数为（　　）

13．一次函数的图象经过点（2，1）和（-1，-3），则它的解析式为（　　）

A．

$y=\frac{3}{4}x-\frac{5}{3}$

B．

$y=\frac{4}{3}x-\frac{3}{5}$

C．

$y=\frac{3}{4}x+\frac{3}{5}$

D．

$y=\frac{4}{3}x-\frac{5}{3}$

10．分式化简：
（1）${（\frac{{{a^2}b}}{-c}）^3}•{（\frac{c^2}{ab}）^2}÷{（\frac{bc}{a}）^4}$
（2）$（\frac{2x}{x-2}-\frac{x}{x+2}）÷\frac{x}{{{x^2}-4}}$．

11．顺次连结对角线垂直的四边形各边中点，所得四边形是（　　）

试题分类