题目内容
6.作图题:如图是单位长度为1的正方形网格.(1)在图1中画出一条以格点为端点,长度为$\sqrt{10}$的线段AB;
(2)在图2中画出一个以格点为顶点,面积为5的正方形ABCD.
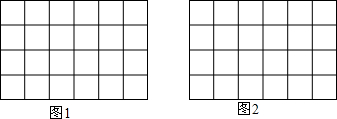
分析 (1)由勾股定理得出$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,画出线段AB即可;
(2)由勾股定理得出$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,画出正方形ABCD即可.
解答 解:(1)由勾股定理得:
$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$
如图1所示,
线段AB即为所求;
(2)由勾股定理得:
$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
正方形ABCD如图2所示.
点评 本题考查了正方形的性质、勾股定理;熟练掌握勾股定理,并能进行计算与作图是解决问题的关键.

练习册系列答案
相关题目
1.下列图案中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
18.在Rt△ABC中,∠C=90°,∠B=30°,斜边AB的长为2,则AC长为( )
| A. | 4 | B. | 2 | C. | 1 | D. | $\frac{1}{2}$ |
15.若abc<0,且ac>0,则下列各式一定正确的是( )
| A. | ac+b>0 | B. | ac-b>0 | C. | ac+b<0 | D. | ac-b<0 |
 已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E.当AE=BC时,则∠A的度数为20°.
已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E.当AE=BC时,则∠A的度数为20°. 有一数值转换机,原理如图所示,若输入的x的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,请你探索第2014次输出的结果是1.
有一数值转换机,原理如图所示,若输入的x的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,请你探索第2014次输出的结果是1.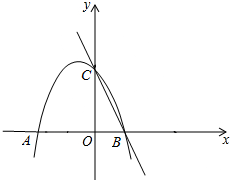 如图,抛物线y=-$\frac{1}{2}$x2-$\frac{1}{2}$x+3与x轴交于A、B两点,与y轴交于点C.
如图,抛物线y=-$\frac{1}{2}$x2-$\frac{1}{2}$x+3与x轴交于A、B两点,与y轴交于点C.