题目内容
3.点P(-2,y1)和点Q(-1,y2)分别为抛物线y=x2-4x+3上的两点,则y1>y2. (用“>”或“<”填空).分析 先根据函数解析式确定出对称轴为直线x=2,再根据二次函数的增减性,x<2时,y随x的增大而减小解答.
解答 解:∵y=x2-4x+3=(x-2)2-1,
∴二次函数图象的对称轴为直线x=2,
∵2>-1>-2,
∴y1>y2.
故答案为:>.
点评 本题考查了二次函数图象上点的坐标特征,主要利用了二次函数的增减性,求出对称轴解析式是解题的关键.

练习册系列答案
相关题目
14.将抛物线y=2x2+1绕原点O旋转180°,则旋转后的抛物线的解析式为( )
| A. | y=-2x2 | B. | y=-2x2+1 | C. | y=2x2-1 | D. | y=-2x2-1 |
18.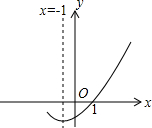 已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论正确的有( )个.①a+b+c=0;②ax2+bx+c=0的两根分别为-3和1;③b>2a;④a-2b+c>0.
已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论正确的有( )个.①a+b+c=0;②ax2+bx+c=0的两根分别为-3和1;③b>2a;④a-2b+c>0.
 已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论正确的有( )个.①a+b+c=0;②ax2+bx+c=0的两根分别为-3和1;③b>2a;④a-2b+c>0.
已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论正确的有( )个.①a+b+c=0;②ax2+bx+c=0的两根分别为-3和1;③b>2a;④a-2b+c>0.| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
13. 如图所示,△ABC绕点A旋转至△AEF,其旋转角是( )
如图所示,△ABC绕点A旋转至△AEF,其旋转角是( )
 如图所示,△ABC绕点A旋转至△AEF,其旋转角是( )
如图所示,△ABC绕点A旋转至△AEF,其旋转角是( )| A. | ∠BAE | B. | ∠CAE | C. | ∠EAF | D. | ∠BAF |
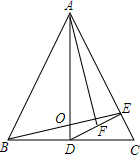 如图,在等腰△ABC中,AB=AC,AD⊥BC,垂足为D,DE⊥AC,垂足为E,且DF=EF,求证:AF⊥BE.
如图,在等腰△ABC中,AB=AC,AD⊥BC,垂足为D,DE⊥AC,垂足为E,且DF=EF,求证:AF⊥BE.