题目内容

18．某长方形足球场的周长是310米，长和宽之差为25米，求这个足球场的长和宽．如果设这个足球场的宽为x米，那么它的长为（x+25）米，由此可建立的方程模型为2（x+x+25）=310．

分析 本题隐含的等量关系：①长-宽=25  ②2×（长+宽）=310，如果设这个足球场的宽为x米，那么它的长为 （x+25）米，再由等量关系②列方程即可．

解答 解：设这个足球场的宽为x米，那么它的长为 （x+25）米，
根据题意可列方程：2（x+x+25）=310
故答案为：（x+25）；2（x+x+25）=310

点评 本题考查了由实际问题抽象出一元一次方程，关键是认真审题，找出题目隐含的等量关系．

练习册系列答案
相关题目
19．已知b=2a+3，求代数式2（2a-b）2-3（2a-b）+20的值．
9．若α，β，γ是方程x3-x-1=0的根，求证：$\frac{α+1}{α-1}$+$\frac{β+1}{β-1}$+$\frac{γ+1}{γ-1}$=7．
6．方程x（x+4）=-3（x+4）的解是x1=-3，x2=-4．
13．已知α是一元二次方程2x2-2x-3=0的两个根中较大的根，则下面对α的估计正确的是（　　）
A．0＜α＜$\frac{1}{2}$B．$\frac{1}{2}$＜α＜1C．1＜α＜$\frac{8}{5}$D．$\frac{8}{5}$＜α＜2
3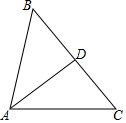．如图，在下列条件中，不能证明△ABD≌△ACD的是（　　）
A．BD=DC，AB=ACB．∠ADB=∠ADC，BD=DCC．∠B=∠C，∠BAD=∠CADD．∠B=∠C，BD=DC
10．已知点（m，n）是正比例函数y=kx（k≠0）上的一点，当m增加2时，n就减小3，则k的值为（　　）
A．2B．-3C．-$\frac{2}{3}$D．-$\frac{3}{2}$
7．如图，大楼AB的高为16米，远处有一塔CD，小李在楼底A处测得塔顶D处的仰角为60°，在楼顶B处测得塔顶D处的仰角为45°，其中A、C两点分别位于B、D两点正下方，且A、C两点在同一水平线上，求塔CD的高度．（结果保留根号）
8．方程x2-121=0的根是（　　）
A．11B．-11C．11或-11D．14或-14

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网