Question

13．如图，在直角坐标系中，四边形OABC为正方形，顶点A，C在坐标轴上，以边AB为弦的⊙M与x轴相切，若点A的坐标为（0，8），则圆形M的坐标为（-4，5）．

Answer 1

分析 如图，作MN⊥AB于N，NM的延长线交于OC于K，连接AM，设⊙M的半径为r，在Rt△AMN中，利用勾股定理列出方程即可解决问题．

解答 解：如图，作MN⊥AB于N，NM的延长线交于OC于K，连接AM．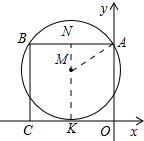

∵四边形ABCD是正方形，
∴∠ABC=∠BCO=90°，∵∠KNB=90°，
∴四边形BCKN是矩形，
∴BC=NK=OA=8，设⊙M的半径为r，
在Rt△AMN中，∵AM²=MN²+AN²，BN=AN=4，MN=8-r，
∴r²=4²+（8-r）²，
∴r=5，
∴点M的坐标为（-4，5）．
故答案为（-4，5）．

点评 本题考查切线的性质、正方形的性质、坐标与图形的性质等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考常考题型．