题目内容
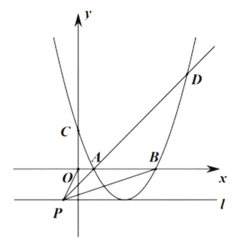
【题目】在![]() 中,
中,![]() ,OA平分
,OA平分![]() 交BC于点O,以O为圆心,OC长为半径作圆交BC于点D.
交BC于点O,以O为圆心,OC长为半径作圆交BC于点D.

(1)如图1,求证:AB为![]() 的切线;
的切线;
(2)如图2,AB与![]() 相切于点E,连接CE交OA于点F.
相切于点E,连接CE交OA于点F.
①试判断线段OA与CE的关系,并说明理由.
②若![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析;(2)①OA垂直平分CE,理由见解析;②![]()
【解析】
(1)过点O作OG⊥AB,垂足为G,利用角平分线的性质定理可得OG=OC,即可证明;
(2)①利用切线长定理,证明OE=OC,结合OE=OC,再利用垂直平分线的判定定理可得结论;
②根据![]() 求出OF和CF,再证明△OCF∽△OAC,求出AC,再证明△BEO∽△BCA,得到
求出OF和CF,再证明△OCF∽△OAC,求出AC,再证明△BEO∽△BCA,得到![]() ,设BO=x,BE=y,可得关于x和y的二元一次方程组,求解可得BO和BE,从而可得结果.
,设BO=x,BE=y,可得关于x和y的二元一次方程组,求解可得BO和BE,从而可得结果.
解:(1)如图,过点O作OG⊥AB,垂足为G,
∵OA平分![]() 交BC于点O,
交BC于点O,
∴OG=OC,
∴点G在![]() 上,
上,
即AB与![]() 相切;
相切;

(2)①OA垂直平分CE,理由是:
连接OE,
∵AB与![]() 相切于点E,AC与
相切于点E,AC与![]() 相切于点C,
相切于点C,
∴AE=AC,
∵OE=OC,
∴OA垂直平分CE;
②∵![]() ,
,
则FC=2OF,在△OCF中,
![]() ,
,
解得:OF=![]() ,则CF=
,则CF=![]() ,
,
由①得:OA⊥CE,
则∠OCF+∠COF=90°,又∠OCF+∠ACF=90°,
∴∠COF=∠ACF,而∠CFO=∠ACO=90°,
∴△OCF∽△OAC,
∴![]() ,即
,即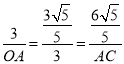 ,
,
解得:AC=6,
∵AB与圆O切于点E,
∴∠BEO=90°,AC=AE=6,而∠B=∠B,
∴△BEO∽△BCA,
∴![]() ,设BO=x,BE=y,
,设BO=x,BE=y,
则![]() ,
,
可得:![]() ,
,
解得:![]() ,即BO=5,BE=4,
,即BO=5,BE=4,
∴tanB=![]() =
=![]() .
.


【题目】小云统计了自己所住小区5月1日至30日的厨余垃圾分出量(单位:千克),相关信息如下:
![]() .小云所住小区5月1日至30日的厨余垃圾分出量统计图:
.小云所住小区5月1日至30日的厨余垃圾分出量统计图:
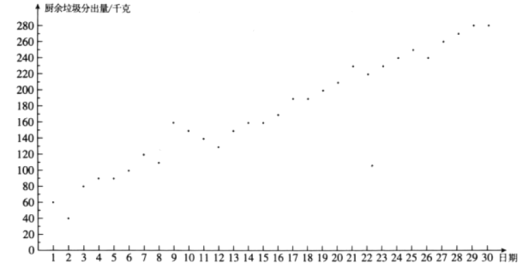
![]() .小云所住小区5月1日至30日分时段的厨余垃圾分出量的平均数如下:
.小云所住小区5月1日至30日分时段的厨余垃圾分出量的平均数如下:
时段 | 1日至10日 | 11日至20日 | 21日至30日 |
平均数 | 100 | 170 | 250 |
(1)该小区5月1日至30日的厨余垃圾分出量的平均数约为 (结果取整数)
(2)已知该小区4月的厨余垃圾分出量的平均数为60,则该小区5月1日至30日的厨余垃圾分出量的平均数约为4月的 倍(结果保留小数点后一位);
(3)记该小区5月1日至10日的厨余垃圾分出量的方差为![]() 5月11日至20日的厨余垃圾分出量的方差为
5月11日至20日的厨余垃圾分出量的方差为![]() ,5月21日至30日的厨余垃圾分出量的方差为
,5月21日至30日的厨余垃圾分出量的方差为![]() .直接写出
.直接写出![]() 的大小关系.
的大小关系.
【题目】从2018年12月初开始,某地环保部门连续一年对![]() 两市的空气质量进行监测,将
两市的空气质量进行监测,将![]() 天的空气污染指数(简称:API)的平均值作为每个月的空气污染指数,
天的空气污染指数(简称:API)的平均值作为每个月的空气污染指数,![]() 个月的空气污染指数如下:
个月的空气污染指数如下:
![]()
![]()
整理、描述数据:
空气质量
按如表整理、描述这两市空气污染指数的数据:
城市 | 空气质量为优 | 空气质量为良 | 空气质量为轻微污染 |
|
|
|
|
|
说明:空气污染指数![]() 时,空气质量为优;
时,空气质量为优;![]() 空气污染指数
空气污染指数![]() 时,空气质量为良;
时,空气质量为良;![]() 空气污染指数
空气污染指数![]() 时,空气质量为轻微污染.
时,空气质量为轻微污染.
分析数据:
两市的空气污染指数的平均数、中位数、众数如下表所示;
城市 | 平均数 | 中位数 | 众数 |
|
|
| |
|
|
|
请将以上两个表格补充完整:
得出结论:可以推断出 市这一年中环境状况比较好,理由_____.(至少从两个不同的角度说明推断的合理性)