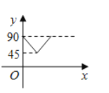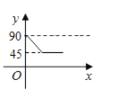��Ŀ����
����Ŀ��ij��ѧ���иֱ��鷨�������Ը��꼶ͬѧ�Ļ����������ͳ�ƣ�������������������������ͳ��ͼ��
����ͼ�������Ϣ����������⣺
(1)����ͳ��ͼ�����Ƚ��������ε�Բ�ĽǵĶ�����______�ȣ�
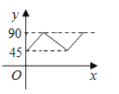
(2)�뽫����ͳ��ͼ��ȫ��
(3)���һ�Ƚ���ͬѧ����![]() �������꼶����
�������꼶����![]() ���Ծ��꼶������ͬѧ�������꼶�������ӻ��һ�Ƚ���ͬѧ����ѡ2�˲μ��м��ֱ��鷨��������ͨ���б�����״ͼ�ķ�������ѡ����2���м��а��꼶ͬѧ���о��꼶ͬѧ�ĸ��ʣ�
���Ծ��꼶������ͬѧ�������꼶�������ӻ��һ�Ƚ���ͬѧ����ѡ2�˲μ��м��ֱ��鷨��������ͨ���б�����״ͼ�ķ�������ѡ����2���м��а��꼶ͬѧ���о��꼶ͬѧ�ĸ��ʣ�
���𰸡�(1)108��(2)��ͼ��������(3)![]() .
.
��������
(1)�ȸ��ݲ��뽱������������ռ�ٷֱ����������������![]() �������Ƚ�������ռ�������ɵô𰸣�(2)�������������һ�Ƚ�����������ȫͼ�μ��ɣ�(3)����״ͼ�ó����еȿ��ܽ�����ٴ����ҵ����������Ľ���������ø��ʹ�ʽ���㼴�ɵô𰸣�
�������Ƚ�������ռ�������ɵô𰸣�(2)�������������һ�Ƚ�����������ȫͼ�μ��ɣ�(3)����״ͼ�ó����еȿ��ܽ�����ٴ����ҵ����������Ľ���������ø��ʹ�ʽ���㼴�ɵô𰸣�
(1)�߱������������Ϊ![]() (��)��
(��)��
������ͳ��ͼ�����Ƚ��������ε�Բ�ĽǵĶ�����![]() ��
��
�ʴ�Ϊ��108��
(2)һ�Ƚ�����Ϊ![]() (��)��
(��)��
��ȫͼ�����£�
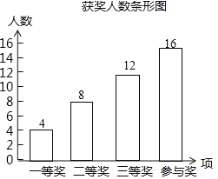
(3)һ�Ƚ��У����꼶����Ϊ![]() (��)�����꼶����Ϊ
(��)�����꼶����Ϊ![]() (��)������꼶����2�ˣ�
(��)������꼶����2�ˣ�
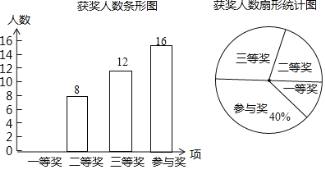
����״ͼ���£�
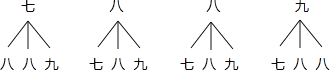
����״ͼ֪������12�ֵȿ��ܽ����������ѡ����2���м��а��꼶ͬѧ���о��꼶ͬѧ����4�ֽ����
������ѡ����2���м��а��꼶ͬѧ���о��꼶ͬѧ�ĸ���Ϊ![]() ��
��

����Ŀ��ijʳƷ������һ�ְ��Ʒʳ�ģ�����![]() ��ǧ��
��ǧ��![]() �����ۼ۸�
�����ۼ۸�![]() Ԫ
Ԫ![]() ǧ��
ǧ��![]() ���㺯����ϵʽ
���㺯����ϵʽ![]() �����г���������Ϣ���֣��ð��Ʒʳ�ĵ��г�������
�����г���������Ϣ���֣��ð��Ʒʳ�ĵ��г�������![]() ��ǧ��
��ǧ��![]() �����ۼ۸�
�����ۼ۸�![]() Ԫ
Ԫ![]() ǧ��
ǧ��![]() ����һ�κ�����ϵ�����±���
����һ�κ�����ϵ�����±���
���ۼ۸� | 2 | 4 |
| 10 |
������� | 12 | 10 |
| 4 |
��֪����۲��Ź涨���ۼ۸�x������2Ԫ![]() ǧ���Ҳ�����10Ԫ
ǧ���Ҳ�����10Ԫ![]() ǧ��
ǧ��
![]() ��q��x�ĺ�����ϵʽ��
��q��x�ĺ�����ϵʽ��
![]() ������С�ڻ�����г�������ʱ�����ְ��Ʒʳ����ȫ���۳������ʱx��ȡֵ��Χ��
������С�ڻ�����г�������ʱ�����ְ��Ʒʳ����ȫ���۳������ʱx��ȡֵ��Χ��
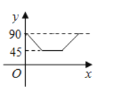
![]() �����������г�������ʱ��ֻ���۳������г��������İ��Ʒʳ�ģ�ʣ���ʳ�����ڱ����ڶ̶�ֻ�ܷ���
�����������г�������ʱ��ֻ���۳������г��������İ��Ʒʳ�ģ�ʣ���ʳ�����ڱ����ڶ̶�ֻ�ܷ���![]() ���ð��Ʒʳ�ĵijɱ���2Ԫ
���ð��Ʒʳ�ĵijɱ���2Ԫ![]() ǧ�ˣ�
ǧ�ˣ�
![]() �һ�õ�����
�һ�õ�����![]() ��Ԫ
��Ԫ![]() �����ۼ۸�x�ĺ�����ϵʽ��
�����ۼ۸�x�ĺ�����ϵʽ��
![]() �����һ�õ�����
�����һ�õ�����![]() ��Ԫ
��Ԫ![]() �����ۼ۸�x�����Ƕ�����ʱ��ֱ��д��x��ȡֵ��Χ
�����ۼ۸�x�����Ƕ�����ʱ��ֱ��д��x��ȡֵ��Χ![]() ����
����![]() �ۼ�
�ۼ�![]() �ɱ�
�ɱ�![]()