题目内容
【题目】如图所示,二次函数![]() 的图像(记为抛物线
的图像(记为抛物线![]() )与y轴交于点C,与x轴分别交于点A、B,点A、B的横坐标分别记为
)与y轴交于点C,与x轴分别交于点A、B,点A、B的横坐标分别记为![]() ,
,![]() ,且
,且![]() .
.
(1)若![]() ,
,![]() ,且过点
,且过点![]() ,求该二次函数的表达式;
,求该二次函数的表达式;
(2)若关于x的一元二次方程![]() 的判别式
的判别式![]() .求证:当
.求证:当![]() 时,二次函数
时,二次函数![]() 的图像与x轴没有交点.
的图像与x轴没有交点.
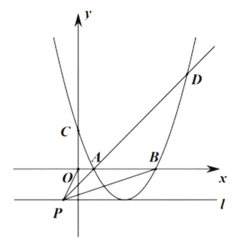
(3)若![]() ,点P的坐标为
,点P的坐标为![]() ,过点P作直线l垂直于y轴,且抛物线的
,过点P作直线l垂直于y轴,且抛物线的![]() 顶点在直线l上,连接OP、AP、BP,PA的延长线与抛物线
顶点在直线l上,连接OP、AP、BP,PA的延长线与抛物线![]() 交于点D,若
交于点D,若![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
(1)根据题意,把![]() ,
,![]() ,点
,点![]() ,代入解析式,即可求出解析式;
,代入解析式,即可求出解析式;
(2)利用根的判别式进行判断,即可得到结论;
(3)根据二次函数的性质,得到![]() ,结合根与系数的关系,得到
,结合根与系数的关系,得到![]() ,然后证明
,然后证明![]() ,得到
,得到![]() ,然后得到
,然后得到![]() ,利用二次根式的性质即可得到答案.
,利用二次根式的性质即可得到答案.
解:(1)由题意得:![]() ,
,
∵函数过点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)由题意,一元二次方程![]() 的判别式
的判别式![]() .
.
∴![]() ,
,
∴![]() ,
,
在函数![]() 中,
中,
![]()
∵![]() ,
,
∴![]() ,
,
即函数图象与x轴没有交点.
(3)因为函数顶点在直线l上,则有![]() ,
,
即![]() ①
①
∵![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
由①得:![]() ②
②
∵![]() ,
,
∴![]()
∵![]() ,
,![]()
∴![]() ,
,
则![]() .
.
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() .
.
由②得:![]() ,
,
∴![]() ,
,
∴当![]() 时,
时,![]() .
.

练习册系列答案
相关题目
【题目】2020年是脱贫攻坚年,为实现全员脱贫目标,某村贫困户在当地政府支持帮助下,办起了养鸡场,经过一段时间精心饲养,总量为3000只的一批鸡可以出售.现从中随机抽取50只,得到它们质量的统计数据如下:
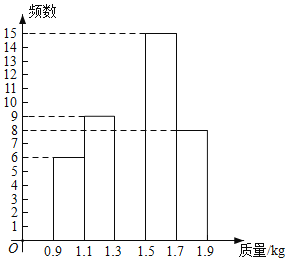
质量 | 组中值 | 数量(只) |
| 1.0 | 6 |
| 1.2 | 9 |
| 1.4 | a |
| 1.6 | 15 |
| 1.8 | 8 |
根据以上信息,解答下列问题:
(1)表中![]() ______,补全频数分布直方图;
______,补全频数分布直方图;
(2)这批鸡中质量不小于![]() 的大约有多少只?
的大约有多少只?
(3)这些贫因户的总收入达到54000元,就能实现全员脱贫目标.按15元![]() 的价格售出这批鸡后,该村贫困户能否脱贫?
的价格售出这批鸡后,该村贫困户能否脱贫?