题目内容
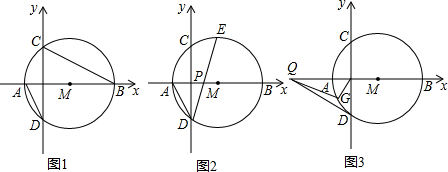
6. 如图,矩形AOBC,点A、B分别在x、y轴上,对角线AB、OC交于点D,点C($\sqrt{3}$,1),点M是射线OC上一动点.
如图,矩形AOBC,点A、B分别在x、y轴上,对角线AB、OC交于点D,点C($\sqrt{3}$,1),点M是射线OC上一动点.(1)求证:△ACD是等边三角形;
(2)若△OAM是等腰三角形,求点M的坐标;
(3)若N是OA上的动点,则MA+MN是否存在最小值?若存在,请求出这个最小值;若不存在,请说明理由.
分析 (1)利用点C坐标,即可求出相应角度,利用矩形性质,即可求出三角形CDA两个内角度数为60°,即可证明三角形是等边三角形.
(2)由等腰三角形性质,对三角形OAM三边关系进行讨论,分别求出三种情况下点M的坐标即可;
(3)做点A关于直线OC对称点,利用对称性可以求出最小值.
解答 解:(1)∵C($\sqrt{3}$,1),
∴AC=1,OA=$\sqrt{3}$,
∴OC=2,
∴∠COA=30°,∠OCA=60°,
∵矩形AOBC,
∴∠ABC=∠OCB=30°,
∴∠ADC=60°,
∴△ACD是等边三角形;
(2)△OAM是等腰三角形,
当OM=MA时,此时点M与点D重合,
∵C($\sqrt{3}$,1),点D为OC中点,
∴M($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$).
当OM1=OA时,做M1E⊥OA,垂足为E,如下图:
∴OM1=OA=$\sqrt{3}$,
由(1)知∠M1OA=30°,
∴M1E=$\frac{\sqrt{3}}{2}$,OE=$\frac{3}{2}$,
∴M1($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$).
当OA=AM2时,做M2F⊥OA,垂足为F,如上图:
AM2=$\sqrt{3}$,
由(1)知∠COA=∠AM2O=30°,
∴∠M2AF=60°,
∴AF=$\frac{\sqrt{3}}{2}$,M2F=$\frac{3}{2}$,
M2($\frac{3\sqrt{3}}{2}$,$\frac{3}{2}$).
综上所述:点M坐标为M($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$)、($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$)、($\frac{3\sqrt{3}}{2}$,$\frac{3}{2}$).
(3)存在,做点A关于直线OC对称点为G,如下图:
则AG⊥OC,且∠GOA=60°,OG=OA=$\sqrt{3}$,
∴ON=$\frac{\sqrt{3}}{2}$,GN=$\frac{3}{2}$,
∵点A、G关于直线OC对称,
∴MG=MA,
∴MA+MN=MG+MN,
∵N是OA上的动点,
∴当GN⊥x轴时,MA+MN最小,
∴存在MA+MN存在最小值,最小值为$\frac{3}{2}$.
点评 题目考查了一次函数综合应用,考查知识点包括:等腰三角形、线段最值、动点问题,解决此类题目关键是找到图形变换的规律,题目整体较难.适合学生压轴训练.

| 玩具型号 | A | B | C |
| 批发价(元/个) | 20 | 24 | 28 |
| 零售价(元/个) | 25 | 30 | 40 |
(1)第一天,该玩具店批发A,B两种型号玩具共59个,用去了1344元钱,这两种型号玩具当天全部售完后一共能赚多少元钱?
(2)第二天,该玩具店用第一天全部售完后的总零售价钱批发A,B,C三种型号玩具中的两种玩具共68个,且当天全部售完,请通过计算说明该玩具店第二天应如何进货才能使全部售完后赚的钱最多?
| A. | 算术平方根等于自身的数只有1 | |
| B. | $\sqrt{\frac{1}{2}}$是最简二次根式 | |
| C. | 有一个角等于60°的三角形是等边三角形 | |
| D. | 两角及其夹边分别相等的两个三角形全等 |
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 不能确定 |
 如图,一次函数y=kx+b的图象与两坐标轴的正半轴相交,则k,b的取值范围是( )
如图,一次函数y=kx+b的图象与两坐标轴的正半轴相交,则k,b的取值范围是( )| A. | k>0,b>0 | B. | k>0,b<0 | C. | k<0,b>0 | D. | k<0,b<0 |