题目内容
 已知二次函数y=-
已知二次函数y=-| 1 |
| 2 |
(1)试确定抛物线的开口方向、顶点坐标和对称轴;
(2)x为何值时,y有最值?
(3)在如图所示的坐标系中,画出函数的图象,并说明该抛物线是由抛物线y=-
| 1 |
| 2 |
(4)根据图象回答,x取何值时,y>0,y=0,y<0?
(5)根据图象回答,x取何值时,y随x的增大而增大?x取何值时,y随x的增大而减小?
考点:二次函数的性质,二次函数的图象,二次函数图象与几何变换,二次函数的最值
专题:
分析:(1)转化抛物线的表达式,即可求出抛物线的开口方向、顶点坐标和对称轴,
(2)由抛物线的表达式可得x为何值时,y有最值.
(3)根据对称轴,顶点及与x轴的交点画图即可,再由几何变换求解即可.
(4)由抛物线与x轴的交点可判定x取何值时,y>0,y=0,y<0.
(5)由抛物线的开口方向向下,对称轴为x=1即可求得.
(2)由抛物线的表达式可得x为何值时,y有最值.
(3)根据对称轴,顶点及与x轴的交点画图即可,再由几何变换求解即可.
(4)由抛物线与x轴的交点可判定x取何值时,y>0,y=0,y<0.
(5)由抛物线的开口方向向下,对称轴为x=1即可求得.
解答:解:y=-
x2+x+4=-
(x-1)2+
.
(1)抛物线的开口方向向下、顶点坐标(1,
),对称轴为x=1;
(2)当x=1时,y有最大值,最大值为
.
(3)如图,
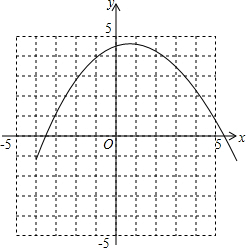
y=-
x2向右平移1个单位,向上平移
个单位即可
(4)由-
x2+x+4=0,解方程可得x1=-
,x2=
,
∴当x<-
或x>
时,y>0,
当x=-
或=
,y=0,
当-
<x<
时,y<0.
(5)当x<1时,y随x的增大而增大,
当x>1时,y随x的增大而减小.
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
(1)抛物线的开口方向向下、顶点坐标(1,
| 9 |
| 2 |
(2)当x=1时,y有最大值,最大值为
| 9 |
| 2 |
(3)如图,

y=-
| 1 |
| 2 |
| 9 |
| 2 |
(4)由-
| 1 |
| 2 |
| 7 |
| 2 |
| 11 |
| 2 |
∴当x<-
| 7 |
| 2 |
| 11 |
| 2 |
当x=-
| 7 |
| 2 |
| 11 |
| 2 |
当-
| 7 |
| 2 |
| 11 |
| 2 |
(5)当x<1时,y随x的增大而增大,
当x>1时,y随x的增大而减小.
点评:本题主要考查了二次函数的性质,解题的关键是熟记二次函数的性质.

练习册系列答案
相关题目
下列说法中,正确的有( )
①无限小数都是无理数;②无理数都是无限小数;
③带根号的数都是无理数;④-3是9的一个平方根.
①无限小数都是无理数;②无理数都是无限小数;
③带根号的数都是无理数;④-3是9的一个平方根.
| A、0个 | B、1个 | C、2个 | D、3个 |
若m=2,|n|=3,则m+n=( )
| A、5 | B、-5 |
| C、-1或5 | D、1或5 |
 如图,已知Rt△ABC中,∠C=90°,AC=8cm,BC=6cm.现将△ABC进行折叠,使顶点A,B重合,则折痕DE=
如图,已知Rt△ABC中,∠C=90°,AC=8cm,BC=6cm.现将△ABC进行折叠,使顶点A,B重合,则折痕DE=
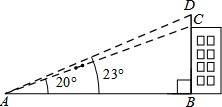 如图,大楼顶上有一根旗杆,杆高CD=3m,某人在点A处测得塔底C的仰角为20°,塔顶D的仰角为23°,求此人距BC的水平距离AB.
如图,大楼顶上有一根旗杆,杆高CD=3m,某人在点A处测得塔底C的仰角为20°,塔顶D的仰角为23°,求此人距BC的水平距离AB.