题目内容
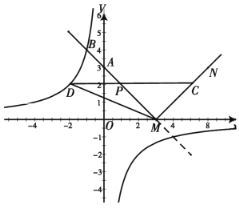
【题目】如图,甲、乙两只捕捞船同时从A港出海捕鱼.甲船以每小时![]() 千米的速度沿西偏北30°方向前进,乙船以每小时15千米的速度沿东北方向前进.甲船航行2小时到达C处,此时甲船发现渔具丢在乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶,结果两船在B处相遇.
千米的速度沿西偏北30°方向前进,乙船以每小时15千米的速度沿东北方向前进.甲船航行2小时到达C处,此时甲船发现渔具丢在乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶,结果两船在B处相遇.
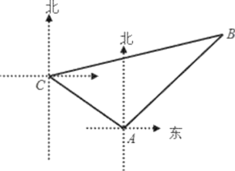
(1)甲船从C处追赶上乙船用了多少时间?
(2)甲船追赶乙船的速度是每小时多少千米?
【答案】(1)2小时;(2)甲船追赶乙船的速度是每小时15+15![]() 千米
千米
【解析】
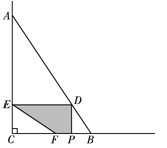
(1)根据方向角可以得到∠BCA=45°,∠B=30度,过A作AD⊥BC于点D,在直角△ACD中,根据三角函数就可求得AD的长,再在直角△ABD中,根据三角函数即可求得AB的长,就可求得时间;
(2)求出BC的长,根据(1)中的结果求得时间,即可求得速度.
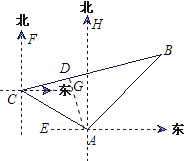
解:(1)如图,过A作AD⊥BC于点D.作CG∥AE交AD于点G.
∵乙船沿东北方向前进,
∴∠HAB=45°,
∵∠EAC=30°,
∴∠CAH=90°-30°=60°
∴∠CAB=60°+45°=105°.
∵CG∥EA,∴∠GCA=∠EAC=30°.
∵∠FCD=75°,∴∠BCG=15°,∠BCA=15°+30°=45°,
∴∠B=180°-∠BCA-∠CAB=30°.
在直角△ACD中,∠ACD=45°,AC=2×15![]() =30
=30![]() ,
,
AD=ACsin45°=3![]() ×
×![]() =30千米.
=30千米.
CD=ACcos45°=30千米.
在直角△ABD中,∠B=30°.
则AB=2AD=60千米.
则甲船从C处追赶上乙船的时间是:60÷15-2=2小时;
(2)BC=CD+BD=30+30![]() 千米.
千米.
则甲船追赶乙船的速度是每小时(30+30![]() )÷2=15+15
)÷2=15+15![]() 千米/小时.
千米/小时.
答:甲船从C处追赶上乙船用了2小时,甲船追赶乙船的速度是每小时15+15![]() 千米.
千米.

 阅读快车系列答案
阅读快车系列答案【题目】为了帮助遭受自然灾害的地区,某学校号召同学们自愿捐款,已知第一次捐款总额为5800元,第二次捐款总额6000元,第二次捐款人数比第一次多20人,而且两次人均捐款额正好相等.
|
| |
每桶容积(升) | 20 | 15 |
每桶价格(元) | 5.6 | 4.5 |
(1)求两次各有多少人捐款?
(2)民政部门要求将捐款换成实物,统一运送到灾区.学校决定将捐款用于购买桶装水现有![]() 两种型号桶装水,上表是这两种桶装水的容积和单价.学校按民政局的救灾规划需订购总容积为40000升的桶装水,用同学们的捐款至少需订购
两种型号桶装水,上表是这两种桶装水的容积和单价.学校按民政局的救灾规划需订购总容积为40000升的桶装水,用同学们的捐款至少需订购![]() 型水多少桶.
型水多少桶.