题目内容
【题目】已知抛物线y＝ax2+bx+c经过点A，点B，与y轴负半轴交于点C，且OC＝OB，其中B点坐标为（3，0），对称轴为直线x＝
．
（1）求抛物线的解析式；
（2）在x轴上方有一点P（m，n），连接PA后满足∠PAB＝∠CAB，记△PBC面积为S，求S与m的函数关系；
（3）在（2）的条件下，当点P恰好落在抛物上时，将直线BC上下平移，平移后的直线y＝x+t与抛物线交于C'，B'两点（C'在B'的左侧），若以点C'、B'、P为顶点三角形是直角三角形，求t的值．
【答案】（1）
；（2）S＝
m+9（m＞﹣2）；（3）t的值为19或32．
【解析】
(1)先确定出点A坐标，再用待定系数法即可得出结论；
(2)先确定出直线AP的解析式，进而用m表示点P的坐标，即可得出结论；
(3)先确定出点P的坐标，当∠B'PC'=90°时，利用根与系数的关系确定出B'C'的中点E的坐标，利用B'C'=2PE建立方程求解，当∠PC'B'=90°时，先确定出点G的坐标，进而求出直线C'G的解析式，进而得出点C'的坐标，即可得出结论．
(1)∵B(3，0)，对称轴为直线x=
，
∴A(﹣2，0)，
∴设抛物线的解析式为y=a(x+2)(x﹣3)=ax2﹣ax﹣6a，
∵B(3，0)，
∴OB=3，
∵OC=OB，
∴OC=3，
∴C(0，﹣3)，
把C(0，﹣3)代入y=a(x+2)(x﹣3)，
∴﹣6a=﹣3，
∴a=，
∴抛物线的解析式为；
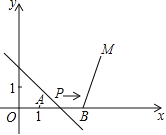
(2)如图1，射线AP与y轴的交点记作点C'，
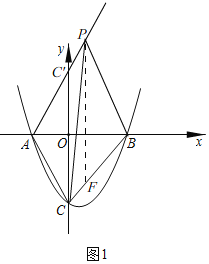
∵∠BAC=∠BAC'，OA=OA，∠AOC=∠AOC'=90°，
∴△AOC≌△AOC'(ASA)，
∴OC'=OC=3，
∴C'(0，3)，
∵A(﹣2，0)，
设直线AP的解析式为
，
∵
，
解得：
，
∴直线AP的解析式为y=
x+3，
∵点P(m，n)在直线AP上，
∴n=m+3，
∵B(3，0)，C(0，﹣3)，
直线BC的解析式为
，
∴
，
解得：
，
∴直线BC的解析式为y=x﹣3，
过点P作y轴的平行线交BC于F，
∴F(m，m﹣3)，
∴PF=m+3﹣(m﹣3)=m+6，
∴S=S△PBC=OBPF=×3(m+6)=m+9(m＞﹣2)；
(3)由(1)知，抛物线的解析式为y=x2﹣x﹣3①
由(2)知，直线AP的解析式为y=x+3②，
联立①②解得，
或
，
∴P(6，12)，
如图2，
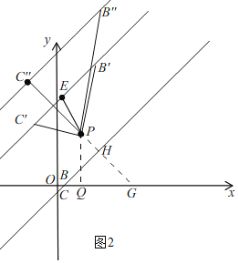
当∠C'PB'=90°时，取B'C'的中点E，连接PE，
则B'C'=2PE，即：B'C'2=4PE2，
设B'(x1，y1)，C'(x2，y2)，
∵直线B'C'的解析式为y=x+t③，
联立①③化简得，x2﹣3x﹣(2t+6)=0，
∴x1+x2=3，x1x2=﹣(2t+6)，
∴点E(，+t)，
B'C'2=(x1﹣x2)2+(y1﹣y2)2=2(x1﹣x2)2=2[(x1+x2)2﹣4x1x2]
=2[9+4(2t+6)]=16t+66，
而PE2=(6﹣
)2+(12﹣﹣t)2=t2﹣21t+
，
∴16t+66=4(t2﹣21t+)，
∴t=6(此时，恰好过点P，舍去)或t=19，
当∠P
=90°时，延长
P交BC于H，交x轴于G，
则∠BHG=90°，
∵OB=CO，∠BOC=90°，
∴∠OBC=45°，
∴∠PGO=45°，
过点P作PQ⊥x轴于Q，则GQ=PQ=12，
∴OG=OQ+GQ=18，
∴点G(18，0)，
∴直线C'G的解析式为y=﹣x+18④，
联立①④解得或
∴C'的坐标为(﹣7，25)，
将点C'坐标代入y=x+t中，得25=﹣7+t，
∴t=32，
即：满足条件的t的值为19或32．
