题目内容
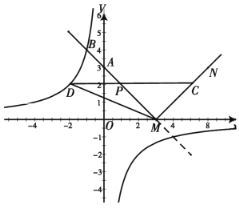
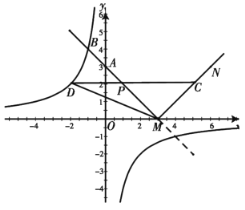
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且与双曲线
,且与双曲线![]() 的一个交点为
的一个交点为![]() ,将直线
,将直线![]() 在
在![]() 轴下方的部分沿
轴下方的部分沿![]() 轴翻折,得到一个“
轴翻折,得到一个“![]() ”形折线
”形折线![]() 的新函数.若点
的新函数.若点![]() 是线段
是线段![]() 上一动点(不包括端点),过点
上一动点(不包括端点),过点![]() 作
作![]() 轴的平行线,与新函数交于另一点
轴的平行线,与新函数交于另一点![]() ,与双曲线交于点
,与双曲线交于点![]() .
.
(1)若点![]() 的横坐标为
的横坐标为![]() ,求
,求![]() 的面积;(用含
的面积;(用含![]() 的式子表示)
的式子表示)
(2)探索:在点![]() 的运动过程中,四边形
的运动过程中,四边形![]() 能否为平行四边形?若能,求出此时点
能否为平行四边形?若能,求出此时点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
【答案】(1)![]() ;(2)不能成为平行四边形,理由见解析
;(2)不能成为平行四边形,理由见解析
【解析】
(1)将点B坐标代入一次函数![]() 上可得出点B的坐标,由点B的坐标,利用待定系数法可求出反比例函数解析式,根据
上可得出点B的坐标,由点B的坐标,利用待定系数法可求出反比例函数解析式,根据![]() 点的坐标为
点的坐标为![]() ,可以判断出
,可以判断出![]() ,再由点P的横坐标可得出点P的坐标是
,再由点P的横坐标可得出点P的坐标是![]() ,结合PD∥x轴可得出点D的坐标,再利用三角形的面积公式即可用含
,结合PD∥x轴可得出点D的坐标,再利用三角形的面积公式即可用含![]() 的式子表示出△MPD的面积;
的式子表示出△MPD的面积;
(2)当P为BM的中点时,利用中点坐标公式可得出点P的坐标,结合PD∥x轴可得出点D的坐标,由折叠的性质可得出直线MN的解析式,利用一次函数图象上点的坐标特征可得出点C的坐标,由点P,C,D的坐标可得出PD≠PC,由此即可得出四边形BDMC不能成为平行四边形.
解:(1)∵点![]() 在直线
在直线![]() 上,
上,
∴![]() .
.
∵点![]() 在
在![]() 的图像上,
的图像上,
∴![]() ,∴
,∴![]() .
.
设![]() ,
,
则![]() .
.
∵![]() ∴
∴![]() .
.
记![]() 的面积为
的面积为![]() ,
,
∴![]()
![]() .
.
(2)当点![]() 为
为![]() 中点时,其坐标为
中点时,其坐标为![]() ,
,
∴![]() .
.
∵直线![]() 在
在![]() 轴下方的部分沿
轴下方的部分沿![]() 轴翻折得
轴翻折得![]() 表示的函数表达式是:
表示的函数表达式是:![]() ,
,
∴![]() ,
,
∴![]() ,
,![]()
∴![]() 与
与![]() 不能互相平分,
不能互相平分,
∴四边形不能成为平行四边形.

 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案【题目】南宁海吉星水果批发市场李大姐家的水果店销售三华李,根据前段时间的销售经验,每天的售价![]() (元/箱)与销售量
(元/箱)与销售量![]() (箱)有如表关系,且已知
(箱)有如表关系,且已知 ![]() 与 x 之间的函数关系是一次函数.
与 x 之间的函数关系是一次函数.
每箱售价x(元) | 68 | 67 | 66 | 65 | … | 40 |
每天销量y(箱) | 40 | 45 | 50 | 55 | … | 180 |
(1)求y 与x的函数解析式;
(2)三华李的进价是 40 元/箱,如果设每天获得的盈利为 ![]() 元,要使该店每天获得最大盈利,则每箱售价多少元?
元,要使该店每天获得最大盈利,则每箱售价多少元?
(3)4 月份(按 30 天算)连续阴雨,销售量减少.该店决定采取降价销售,故在(2)的条件下销售了 18 天之后,三华李开始降价,售价比之前下降了![]() ,同时三华李的进价降为 29 元/箱,销售量也因此比原来每天获得最大盈利时上涨了
,同时三华李的进价降为 29 元/箱,销售量也因此比原来每天获得最大盈利时上涨了![]() ,降价销售了 12 天的三华李销售总盈利比降价销售前的销售总盈利少 5670 元,求
,降价销售了 12 天的三华李销售总盈利比降价销售前的销售总盈利少 5670 元,求![]() 的值.
的值.