题目内容
已知：如图，△ABC≌△ADE，则AB=考点：全等三角形的性质
专题：
分析：根据全等三角形对应边相等，全等三角形对应角相等解答；
先求出∠DAE，再根据全等三角形对应角相等可得∠BAC=∠DAE．
先求出∠DAE，再根据全等三角形对应角相等可得∠BAC=∠DAE．
解答：解：∵△ABC≌△ADE，
∴AB=AD，∠E=∠C．
∵∠BAE=110°，∠BAD=40°，
∴∠DAE=∠BAE-∠BAD=110°-40°=70°，
∵△ABC≌△ADE，
∴∠BAC=∠DAE=70°．
故答案为：AD；C；70．
∴AB=AD，∠E=∠C．
∵∠BAE=110°，∠BAD=40°，
∴∠DAE=∠BAE-∠BAD=110°-40°=70°，
∵△ABC≌△ADE，
∴∠BAC=∠DAE=70°．
故答案为：AD；C；70．
点评：本题考查了全等三角形的性质，熟记性质并准确识图是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知一元二次方程x2-8x+15=0的两个解恰好分别是Rt△ABC的两边长，则第3条边长为（ ）
| A、3 | ||
| B、4 | ||
| C、5 | ||
D、4或
|
在平面直角坐标系中，点P从原点O出发，每次向上平移2个单位长度或向右平移1个单位长度．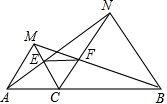
已知：如图，点C为线段AB上一点，△ACM，△CBN都是等边三角形，AN交MC于点E，BM交CN于点F．把a精确到百分位得到的近似数是5.18，则下列不可能是a的值的是（ ）
| A、5.178 |
| B、5.183 |
| C、5.189 |
| D、5.175 |
