题目内容
20.如图1,在△ABC中,AB=AC,G为三角形外一点,且△GBC为等边三角形.(1)求证:直线AG垂直平分BC;
(2)以AB为一边作等边△ABE(如图2),连接EG、EC,试判断△EGC是否构成直角三角形?请说明理由.

分析 (1)由GB=GC,得出点G在BC的垂直平分线上,同理得出点A在BC的垂直平分线上,即可得出结论;
(2)由等边三角形的性质得出GB=BC=GC,EB=BA,∠EBA=∠GBC=∠BGC=∠BCG=60°,证出∠EBC=∠ABG,由SAS证明△EBC≌△ABG,得出∠ECB=∠AGB,再由等腰三角形的性质即可得出结论.
解答 (1)证明:∵△GBC为等边三角形,
∴GB=GC,
∴点G在BC的垂直平分线上,
又∵AB=AC,
∴点A在BC的垂直平分线上,
∴直线AG垂直平分BC;
(2)解:△EGC能构成直角三角形;理由如下:
∵△GBC和△ABE为等边三角形,
∴GB=BC=GC,EB=BA,∠EBA=∠GBC=∠BGC=∠BCG=60°,
∴∠EBC=∠ABG,
在△EBC和△ABG中,
$\left\{\begin{array}{l}{EB=BA}&{\;}\\{∠EBC=∠ABG}&{\;}\\{BC=GB}&{\;}\end{array}\right.$,
∴△EBC≌△ABG(SAS),
∴∠ECB=∠AGB,
∵GB=GC且AG⊥BC,
∴∠AGB=$\frac{1}{2}$∠BGC=30°
∴∠ECB=30°,
∴∠ECG=90°,
即△EGC构成直角三角形.
点评 本题考查了全等三角形的判定与性质、等边三角形的性质、线段垂直平分线的判定、等腰三角形的性质;本题综合性强,证明三角形全等是解决(2)的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映,如果调整商品售价,每降价1元,每星期可多卖出20件.设每件商品降价x元后,每星期售出商品的总销售额为y元,则y与x的关系式为( )
| A. | y=60(300+20x) | B. | y=(60-x)(300+20x) | C. | y=300(60-20x) | D. | y=(60-x)(300-20x) |
11.若$\frac{x}{y}$=$\frac{4}{5}$,则$\frac{2x-y}{x+y}$的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | $\frac{3}{2}$ |
8.点P(2,-3)关于x轴对称的点是( )
| A. | (-2,3) | B. | (2,3) | C. | (-2,-3) | D. | (2,-3) |
5. 折成如图正方体后,与下图相同的是( )
折成如图正方体后,与下图相同的是( )
 折成如图正方体后,与下图相同的是( )
折成如图正方体后,与下图相同的是( )| A. |  | B. |  | C. |  | D. |  |
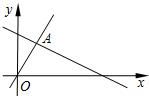 如图,函数y=2x和y=ax+4的图象相交于点A(1,m),则不等式2x<ax+4的解集为x<1.
如图,函数y=2x和y=ax+4的图象相交于点A(1,m),则不等式2x<ax+4的解集为x<1.