题目内容
10. 如图,已知一条直线过点(0,4),且与抛物线y=$\frac{1}{4}$x2交于A,B两点,其中点A的横坐标是-2.
如图,已知一条直线过点(0,4),且与抛物线y=$\frac{1}{4}$x2交于A,B两点,其中点A的横坐标是-2.(1)求这条直线的解析式及点B的坐标;
(2)在x轴上是否存在点C,使得△ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由.
分析 (1)首先求得点A的坐标,然后利用待定系数法确定直线的解析式,从而求得直线与抛物线的交点坐标;
(2)如图1,过点B作BG∥x轴,过点A作AG∥y轴,交点为G,然后分若∠BAC=90°,则AB2+AC2=BC2;若∠ACB=90°,则AB2=AC2+BC2;若∠ABC=90°,则AB2+BC2=AC2三种情况求得m的值,从而确定点C的坐标;
解答 解:(1)∵点A是直线与抛物线的交点,且横坐标为-2,
∴y=$\frac{1}{4}$×(-2)2=1,A点的坐标为(-2,1),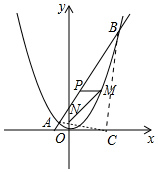
设直线的函数关系式为y=kx+b,
将(0,4),(-2,1)代入得$\left\{\begin{array}{l}{b=4}\\{-2k+b=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{3}{2}}\\{b=4}\end{array}\right.$,
∴直线y=$\frac{3}{2}$x+4,
由$\left\{\begin{array}{l}{y=\frac{3}{2}x+4}\\{y=\frac{1}{4}{x}^{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=8}\\{y=16}\end{array}\right.$
∴点B的坐标为(8,16);
(2)如图,连接AC,BC,
∵由A(-2,1),B(8,16)可求得AB2=325.
设点C(m,0),同理可得AC2=(m+2)2+12=m2+4m+5,
BC2=(m-8)2+162=m2-16m+320,
①若∠BAC=90°,则AB2+AC2=BC2,即325+m2+4m+5=m2-16m+320,
解得:m=-$\frac{1}{2}$;
②若∠ACB=90°,则AB2=AC2+BC2,即325=m2+4m+5+m2-16m+320,
解得:m=0或m=6;
③若∠ABC=90°,则AB2+BC2=AC2,即m2+4m+5=m2-16m+320+325,
解得:m=32;
∴点C的坐标为(-$\frac{1}{2}$,0),(0,0),(6,0),(32,0).
点评 本题是二次函数的综合题型.一次函数的应用、待定系数法、两点间距离公式、勾股定理等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考压轴题.

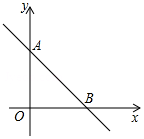 如图,直线y=$\frac{\sqrt{3}}{3}x$+1和x轴、y轴分别交于点A、B.若以线段AB为边作等边三角形ABC,则点C的坐标是($\sqrt{3}$,2)或(0,-1).
如图,直线y=$\frac{\sqrt{3}}{3}x$+1和x轴、y轴分别交于点A、B.若以线段AB为边作等边三角形ABC,则点C的坐标是($\sqrt{3}$,2)或(0,-1). 如图,在线段BF上,有点E、C,BE=CF,∠B=∠F,∠ACB=∠DEF.
如图,在线段BF上,有点E、C,BE=CF,∠B=∠F,∠ACB=∠DEF.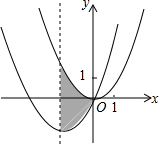 如图,抛物线C1:y=$\frac{1}{2}$x2经过平移得到抛物线C2:y=$\frac{1}{2}$x2+2x,抛物线C2的对称轴与两段抛物线所围成的阴影部分的面积是4.
如图,抛物线C1:y=$\frac{1}{2}$x2经过平移得到抛物线C2:y=$\frac{1}{2}$x2+2x,抛物线C2的对称轴与两段抛物线所围成的阴影部分的面积是4.
 如图,点A位于点O北偏西25°.
如图,点A位于点O北偏西25°.