题目内容
 如图所示,∠B=20°,∠D=40°,∠BCD=2∠A,求∠A的度数.
如图所示,∠B=20°,∠D=40°,∠BCD=2∠A,求∠A的度数.考点:三角形的外角性质,三角形内角和定理
专题:
分析:连接AC并延长,根据三角形外角的性质可得∠B+∠BAE=∠BCE,∠D+∠DAC=∠DCE,再把两式相加即可得出结论.
解答: 解:连接AC并延长,
解:连接AC并延长,
∵∠BCE是△ABC的外角,∠DCE是△ACD的外角,
∴∠B+∠BAE=∠BCE①,∠D+∠DAC=∠DCE②,
①+②得,∠B+∠C+∠BAD=∠BCD,
∵∠B=20°,∠D=40°,∠BCD=2∠A,
∴20°+40°=∠A,即∠A=60°.
 解:连接AC并延长,
解:连接AC并延长,∵∠BCE是△ABC的外角,∠DCE是△ACD的外角,
∴∠B+∠BAE=∠BCE①,∠D+∠DAC=∠DCE②,
①+②得,∠B+∠C+∠BAD=∠BCD,
∵∠B=20°,∠D=40°,∠BCD=2∠A,
∴20°+40°=∠A,即∠A=60°.
点评:本题考查是三角形外角的性质,熟知三角形的一个外角等于和它不相邻的两个内角的和是解答此题的关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
下列选项中,与x2y是同类项的是( )
| A、.-2x2y |
| B、-2xy2 |
| C、xy |
| D、x2y2 |
在-2,-|-6|,-(-5),-32,(-2)2,2-1,(-1)0中正数的个数为( )
| A、2个 | B、3个 | C、4个 | D、5个 |
 如图,若直线AB,CD交于点O,∠AOC:∠AOD=1:5,OE⊥AB,则∠EOC=( )
如图,若直线AB,CD交于点O,∠AOC:∠AOD=1:5,OE⊥AB,则∠EOC=( )| A、100° | B、110° |
| C、120° | D、130° |
下列运算正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
2012年5月25日有700多位来自全国各地的知名企业家聚首湖北共同签约项目,投资总额909000000000元.将909000000000元用科学记数法表示,正确的是( )
| A、909×109元 |
| B、9.09×1011元 |
| C、9.09×1010元 |
| D、9.09×1012元 |
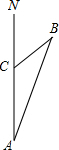 一船上午9时从海岛A出发一20海里/时的速度向正北方向向航行,11时到达B处,从A,B两处分别望灯塔C,测得∠NBA=30°,∠NCB=45°,求从B处到灯塔C的距离.
一船上午9时从海岛A出发一20海里/时的速度向正北方向向航行,11时到达B处,从A,B两处分别望灯塔C,测得∠NBA=30°,∠NCB=45°,求从B处到灯塔C的距离. 如图,已知∠1=∠2,∠B=80°,求∠BCD的度数.
如图,已知∠1=∠2,∠B=80°,求∠BCD的度数.