题目内容
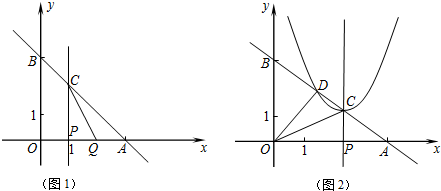
12.已知直线y=kx+6(k<0)分别交x轴、y轴于A、B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒2个单位长度,过点P作x轴的垂线交直线AB于点C,设运动时间为t秒.(1)当k=-1时,线段OA上另有一动点Q由点A向点O运动,它与点P以相同速度同时出发,当点P到达点A时两点同时停止运动(如图1).
①直接写出t=1秒时C、Q两点的坐标;
②若以Q、C、A为顶点的三角形与△AOB相似,求t的值.
(2)当k=-$\frac{3}{4}$时,设以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D(如图2),①求CD的长; ②设△COD的OC边上的高为h,当t为何值时,h的值最大?
分析 (1)①求出函数解析式,求出A、B的坐标,当t=1,求出OP=2,AQ=2,从而得到C,Q的解析式;
②由题意得,P(2t,0),C(2t,-2t+6),Q(6-2t,0),分两种情况讨论:情形一:当△AQC∽△AOB时,∠AQC=∠AOB=90°;情形二:当△ACQ∽△AOB时,∠ACQ=∠AOB=90°.
(2)①由题意得:C(2t,-$\frac{3}{2}$t+6),根据△DEC∽△AOB,得到$\frac{DE}{AO}$=$\frac{CD}{BA}$,求出CD的长;
②S△COD为定值,要使OC边上的高h的值最大,只要OC最短,当OC⊥AB时,OC最短,此时OC的长为$\frac{24}{5}$,判断出Rt△PCO∽Rt△OAB,得到$\frac{OP}{BO}$=$\frac{OC}{BA}$,解答即可.
解答 解:(1)当k=-1时,直线为y=-x+6,可知,A(6,0),B(0,6),
①t=1时,OP=2,得C(2,4);AQ=2,得Q(4,0).
②由题意得,P(2t,0),C(2t,-2t+6),Q(6-2t,0),
分两种情况讨论:情形一:当△AQC∽△AOB时,∠AQC=∠AOB=90°,
∴CQ⊥OA,
∵CP⊥OA,
∴点P与点Q重合,OQ=OP,即6-2t=2t,
∴t=1.5.
情形二:当△ACQ∽△AOB时,∠ACQ=∠AOB=90°,
∵OA=OB=6,
∴△AOB是等腰直角三角形,
∴△ACO也是等腰直角三角形,
∵CP⊥OA,
∴AQ=2CP,即2t=2(-2t+6),
∴t=2,
∴满足条件的t的值是1.5秒或2秒.
(2)①由题意得:C(2t,-$\frac{3}{2}$t+6),
∴以C为顶点的抛物线解析式是y=(x-2t)2-$\frac{3}{2}$t+6,
由(x-2t)2-$\frac{3}{2}$t+6=-$\frac{3}{4}$x+6,
解得x1=2t,x2=2t-$\frac{3}{4}$,
过点D作DE⊥CP于点E,则∠DEC=∠AOB=90°
∵DE∥OA,
∴∠EDC=∠OAB,
∴△DEC∽△AOB,
∴$\frac{DE}{AO}$=$\frac{CD}{BA}$,
∵AO=8,AB=10,
∵AO=8,AB=10,
DE=2t-(2t-$\frac{3}{4}$)=$\frac{3}{4}$,
∴CD=$\frac{DE×BA}{AO}$=$\frac{\frac{3}{4}×10}{8}$=$\frac{15}{16}$
②∵CD=$\frac{15}{16}$,
CD边上的高=$\frac{6×8}{10}$=$\frac{24}{5}$,
∴S△COD=$\frac{1}{2}$×$\frac{15}{16}$×$\frac{24}{5}$=$\frac{9}{4}$,
∴S△COD为定值,要使OC边上的高h的值最大,只要OC最短,当OC⊥AB时,OC最短,此时OC的长为$\frac{24}{5}$,∠BCO=90°,
∵∠AOB=90°,
∴∠COP=90°-∠BOC=∠OBA,
又∵CP⊥OA,
∴Rt△PCO∽Rt△OAB.
∴$\frac{OP}{BO}$=$\frac{OC}{BA}$,
OP=$\frac{OC×OB}{BA}$=$\frac{\frac{24}{5}×6}{10}$=$\frac{72}{25}$,
2t=$\frac{72}{25}$,
∴t=$\frac{36}{25}$,
∴当t为$\frac{36}{25}$秒时,h的值最大.
点评 本题考查了二次函数综合题,涉及动点问题、相似三角形的判定和性质、二次函数的最值等知识,综合性强,在求有关动点问题时要注意分析题意分情况讨论结果.

 如图所示,∠AOC=∠BDO=90°,若∠AOB=150°,则∠DOC的度数为( )
如图所示,∠AOC=∠BDO=90°,若∠AOB=150°,则∠DOC的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
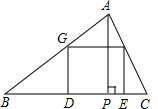 如图,△ABC是一块余料,BC=12cm,高AP=8cm.要把它加工成一块正方形材料,使正方形一边在BC上,其余两个顶点分别在AC、AB上.求这个正方形的边长是多少?
如图,△ABC是一块余料,BC=12cm,高AP=8cm.要把它加工成一块正方形材料,使正方形一边在BC上,其余两个顶点分别在AC、AB上.求这个正方形的边长是多少?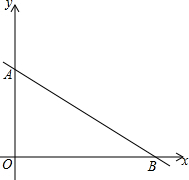 如图,一次函数y=-$\frac{3}{4}$x+6的图象分别与y轴、x轴交于点A、B,点P从点B出发,沿BA以每秒1个单位的速度向点A运动,当点P到达点A时停止运动,设点P的运动时间为t秒.
如图,一次函数y=-$\frac{3}{4}$x+6的图象分别与y轴、x轴交于点A、B,点P从点B出发,沿BA以每秒1个单位的速度向点A运动,当点P到达点A时停止运动,设点P的运动时间为t秒. 按下列语句画出图形
按下列语句画出图形 如图,AB=CD,AD=CB,试证明:AD∥BC.
如图,AB=CD,AD=CB,试证明:AD∥BC. 如图,等腰直角三角形ABC,∠A=90°,D是BC中点,E为AB上一点,且EA=CF,求证:DE=DF.
如图,等腰直角三角形ABC,∠A=90°,D是BC中点,E为AB上一点,且EA=CF,求证:DE=DF.