题目内容
14．计算：（-$\frac{1}{2}$）-1-（π-2015）0+$\sqrt{3}$tan30°．分析 本题涉及负整数指数幂、零指数幂、乘方、特殊角的三角函数值、二次根式化简四个考点．针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果．
解答 解：（-$\frac{1}{2}$）-1-（π-2015）0+$\sqrt{3}$tan30°
=-2-1+$\sqrt{3}$×$\frac{\sqrt{3}}{3}$
=-2-1+1
=-2．
点评 本题考查实数的综合运算能力，是各地中考题中常见的计算题型．解决此类题目的关键是熟记特殊角的三角函数值，熟练掌握负整数指数幂、零指数幂、二次根式等考点的运算．
练习册系列答案
名校课堂系列答案
相关题目
（1）先化简，再求值：$\frac{{x}^{2}-2x}{x-1}$-$\frac{1}{1-x}$，其中x=2015．
2．
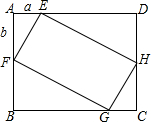如图，在矩形ABCD中，AB=4，BC=5，点E、F、G、H分别在已知矩形的四条边上，且四边形EFGH也是矩形，GF=2EF．若设AE=a，AF=b，则a与b满足的关系为（ ）
如图，在矩形ABCD中，AB=4，BC=5，点E、F、G、H分别在已知矩形的四条边上，且四边形EFGH也是矩形，GF=2EF．若设AE=a，AF=b，则a与b满足的关系为（ ）| A． | $\left\{\begin{array}{l}{a+b=4}\\{a+2b=5}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{2a+b=4}\\{a+2b=5}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{a=2b}\\{2a+b=5}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{2a+b=5}\\{a+2b=4}\end{array}\right.$ |
9．4的平方根是（ ）
| A． | ±2 | B． | 16 | C． | -2 | D． | 2 |
19．
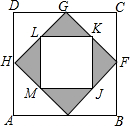如图，顺次连接正方形ABCD各边的中点得到四边形EFGH，顺次连接四边形EFGH各边的中点得到四边形JKLM，若向正方形ABCD中随机撒一粒豆子，则它落在阴影部分的概率是（ ）
如图，顺次连接正方形ABCD各边的中点得到四边形EFGH，顺次连接四边形EFGH各边的中点得到四边形JKLM，若向正方形ABCD中随机撒一粒豆子，则它落在阴影部分的概率是（ ）| A． | $\frac{1}{3}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
3．观察下列各数：1，$\frac{4}{3}$，$\frac{9}{7}$，$\frac{16}{15}$，…，按你发现的规律计算这列数的第6个数为（ ）
| A． | $\frac{25}{31}$ | B． | $\frac{36}{35}$ | C． | $\frac{4}{7}$ | D． | $\frac{62}{63}$ |
