题目内容
19.如图①,在正方形ABCD中,对角线AC,BD相交于点O,E是线段AC上一点,过点A作直线BE的垂线,垂足为点G,交直线OB于点F,易证:OE=OF(1)如图②,在菱形ABCD中,∠ABC=120°,其他条件不变,线段OE,OF有怎样的数量关系,写出你猜想并给予证明;
(2)若∠BAF=15°,AB=2,则OF=$\sqrt{3}$.
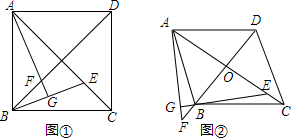
分析 (1)根据菱形的性质得到AB=BC,AC⊥BD,AO=CO,由等腰三角形的性质得到∠ABC=120°,根据三角形的内角和得到∠ACB=∠BAC=30°,于是得到AO=$\sqrt{3}$OB,由对顶角线段得到∠GBF=∠OBE,推出∠AFO=∠OEB,在Rt△AOF中,tan∠AFO=$\frac{AO}{OF}$,在Rt△OBE中,tan∠OEF=$\frac{OB}{OE}$,等量代换得到$\frac{OA}{OF}=\frac{OB}{OE}$,即可得到结论;
(2)根据已知条件得到∠GAE=45°,求得AO=OF,解直角三角形得到AO=AB•cos30°=$\sqrt{3}$,即可得到结论.
解答 解:(1)OF=$\sqrt{3}$OE,
理由:在菱形ABCD中,
∵AB=BC,AC⊥BD,AO=CO,
∴∠BOC=90°,
∵∠ABC=120°,
∴∠ACB=∠BAC=30°,
∴AO=$\sqrt{3}$OB,
∵AG⊥BE,
∴∠BGF=90°,
∵∠GBF=∠OBE,
∴∠AFO=∠OEB,
在Rt△AOF中,tan∠AFO=$\frac{AO}{OF}$,
在Rt△OBE中,tan∠OEF=$\frac{OB}{OE}$,
∴$\frac{OA}{OF}=\frac{OB}{OE}$,
即$\frac{OF}{OE}=\frac{OA}{OB}$=$\sqrt{3}$,
∴OF=$\sqrt{3}$OE;
(2)∵∠OAB=30°,∠GAB=15°,
∴∠GAE=45°,
∵∠AOF=90°,
∴∠F=45°,
∴AO=OF,
∵∠BAO=30°,AB=2,
∴AO=AB•cos30°=$\sqrt{3}$,
∴OF=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查了菱形的性质,正方形的性质,全等三角形的判定和性质,等腰直角三角形的性质,等腰三角形的性质,熟练掌握各定理是解题的关键.

| A. | 2a•4a=8a | B. | a2+a1=a3 | C. | (a2)3=a5 | D. | a1•a1=a2 |
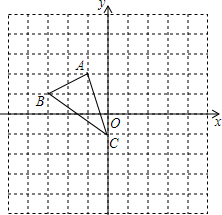 如图,在平面直角坐标系网格中,△ABC的顶点都在格点上,点C坐标(0,-1).
如图,在平面直角坐标系网格中,△ABC的顶点都在格点上,点C坐标(0,-1).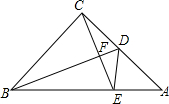 如图,从等腰Rt△ABC的直角顶点C向中线BD作垂线,交BD于点F,交AB于点E,连接DE.求证:∠CDF=∠ADE.
如图,从等腰Rt△ABC的直角顶点C向中线BD作垂线,交BD于点F,交AB于点E,连接DE.求证:∠CDF=∠ADE.